OK, before we go much further, let’s have a brief recap of where we have come so far. (That doesn’t make this a review, though: as I summarize, I’m going to add new categories and terminology.)
We started with doing geometry on the sphere:
We have spent quite a long time on this, actually. It is an important example.
We’ve discussed this, but let me emphasize again: we are considering the sphere as a 2 dimensional space. If we imagine the sphere as the surface of the Earth, for example, it really is only the surface: we are not allowed to travel into the air or below the earth. It is also a mathematical idealization: it is perfectly smooth, perfectly uniform, and has zero thickness. A 2D creature living in the spherical universe has only two independent degrees of freedom: for example, latitude and longitude.
(And one more thing, which didn’t come up before: if we imagine the sphere as a balloon, I am making no distinction between the inner surface of the balloon and the outer surface, because the balloon has no thickness. I am not thinking of the surface as having two sides; a 2D creature occupies the whole thickness of the surface (which is zero). Maybe a transparent sphere might be a better way to picture this.)
The sphere:
- Has a non-Euclidean geometry. For example, there are triangles whose interior angle sums add to more than 180 degrees. The circumference of a circle is less than
. - Has a uniform geometry. There is no way for a 2D creature to tell if it is at the North Pole, or the South Pole, or the Equator, or anywhere in between. In Shape of Space, Weeks calls this a homogeneous geometry. (See p.41 of Weeks.)
- Has positive curvature. I haven’t said this word yet. I’ll be more precise about it soon, but the intuitive idea is that there is “less space” in space than in Euclidean space. Triangles bow outwards, so have internal angle sums bigger than 180 degrees. If we try to draw parallel lines, they get closer to each other as you travel along them, and they eventually meet. The circumference of a circle is smaller than . (Said differently, the circumference of a circle grows less than linearly with its radius.) Traveling around a path, you can turn less than 360 degrees and end up pointing the same way you started.
- Is closed. I haven’t used this word yet either. It means two things: 1) the sphere has no boundary, no edge points; and 2) the sphere is a bounded space, not infinite (the technical word for this is compact, and the exact definition is kind of tricky). See Weeks, pp.42–44.
Just for completeness, let me compare this to the regular old Euclidean plane:
Oh dear. This is quite difficult to draw. I put edges on it, but that would be a rectangle. I am trying to imagine an infinite, perfectly flat plane, which has no thickness: it is perfectly 2 dimensional. As with the sphere, there is no bottom or top of this sheet of paper, because it has no thickness. Any point or line (of zero thickness) takes up the whole thickness of the plane (also zero thickness). Two dimensional beings who live in the Euclidean plane have only two degrees of freedom, for example, North-South and East-West (or if you prefer, left-right and up-down).
The Euclidean plane:
- Has a Euclidean geometry. This means the ordinary rules of geometry that you may have learned before apply. In particular, the internal angles of a triangle always add to 180 degrees, and the circumference of a circle is exactly .
- Has a uniform, or homogeneous, geometry. There is no way for a 2D creature to tell if it is at the place you have picked as an origin, or one hundred miles to the North, South, East, West, or anywhere else.
- Has zero curvature. Euclidean space is the reference point for curvature. Triangles are straight in the ordinary sense, and Euclid’s proofs are valid, so triangles have internal angle sums exactly equal to 180 degrees. Given a line, and a point on the line, there is exactly one parallel line to the first line, passing through the given point. The circumference of a circle is exactly equal to . (Said differently, the circumference of a circle grows exactly linearly with its radius.) Traveling around a path, you must turn exactly 360 degrees in order to end up pointing the same way you started. We will often use the word flat as a synonym for zero curvature.
- Is open. The Euclidean plane is non-compact: it is infinite in extent. It has no boundary: there is no “edge” to the space.
The next thing we looked at was the cube:
The cube. Good ol’ reliable cube.
As before, I am only considering the outer surface of the cube, and considering it to be of idealized zero thickness, so this is also a 2D universe. Two-dimensional creatures living within this space have just two degrees of freedom.
The cube:
- Has a non-Euclidean geometry. For example, there are triangles whose interior angle sums add to more than 180 degrees. The circumference of a circle can be less than . However, it does have Euclidean geometry in some regions. Geometry becomes non-Euclidean if the region you are concerned with contains one or more vertices of the cube.
- Has a non-uniform, or non-homogeneous, geometry. A 2D being could locate the exact position of each vertex: triangles which don’t contain the vertex have internal angle sums of 180 degrees, and triangles which do contain it have sums of 270 degrees: a sudden and dramatic difference. (Also, if the 2D beings have sight, then they are going to see some very funny things near the vertex. I encourage you to think about this; we’ll talk about it soon.)
- Has positive curvature in some places, and zero curvature in others. Triangles, circles, and closed paths which contain one or more vertices behave much like they do on the sphere. Triangles, circles, and closed paths which do not contain any vertex behave exactly as they do in Euclidean space.
- Is singular, or non-smooth. I haven’t used this word yet. The sphere has its curvature smoothly distributed. The curvature of the cube is infinitely compressed into eight discrete points of zero size. Consequently, the sphere is called a smooth space, and the cube is called a singular, or non-smooth space. (For those of you have taken calculus: another word for non-smooth is non-differentiable; the exact definition of smooth involves differentiability.)
- Is closed. It is compact, and has no boundary.
- Is geometrically distinct from, but topologically equivalent to, the sphere. If we ignore geometry, and just pay attention to how things are glued together, the cube is the same as the sphere. In other words, we could continuously deform a sphere to make a cube. As topological spaces, the cube and the sphere are the same. But as geometrical spaces, they are quite different.
Something similar goes for all the other polyhedra we have looked at so far. The only difference is how their curvature has been concentrated: how much curvature per point, and how many points.
Next on our menu is the flat 2D cylinder:
What I am trying to draw here is two parallel straight lines in the Euclidean plane. The points of the “flat cylinder” consist of any points in between those two parallel lines, or lying on the lines. There is an additional rule, that we are “gluing” the two parallel lines. This means that a point P on one line is considered to be the same point as a point P’ on the other line at the same height.
A 2D creature that leaves out the right line, comes back through the left line, without noticing anything has happened.
The 2D flat cylinder:
- Has an everywhere locally Euclidean geometry. I haven’t used the word “locally” yet: it means in a small enough neighborhood. This means the ordinary rules of geometry that you may have learned before apply, as long as things don’t wrap all the way around the cylinder. In particular, the internal angles of a triangle always add to 180 degrees, and the circumference of a circle is exactly , provided that the “hole” of the cylinder is not contained in their interiors.
- Has a uniform, or homogeneous, geometry. There is no way for a 2D creature to tell if it is at the middle of the strip, or the edge, or if it is moved up or down along the strip.
- Has zero curvature. Curvature is a local property. (It is a tricky question of whether I should consider the infinite end, or “hole”, of the cylinder as representing curvature. On the one hand, a triangle containing the “hole” of the cylinder in its interior—that is, one which has an edge that wraps around the cylinder—has an interior angle sum of 540 degrees. On the other hand, the cylinder is not “curved” anywhere. We’ll think about this more later, but for the moment I’ll just say that the cylinder has zero curvature.)
- Is open. It is non-compact: it is infinite in extent. It has no boundary: there is no “edge” to the space.
Now, we could also imagine the cylinder as being rolled up in three dimensions. That is, we could say “cylinder version two” is created by taking the surface of an infinitely long tube in three dimensions:
It’s a bit tricky to draw: because it goes on forever in the up-down direction, I don’t want to put ends on my drawing.
I’m going to assume that I have made the circumference of “cylinder version 2” equal to the width of the strip in my first version, the flat cylinder.
Then, as we have discussed, “cylinder version 2” is geometrically equivalent to the flat cylinder in the first version. Another word for this is to say that the two spaces are isometric (“iso” means “same”, “metric” means measure (like in “geometric”)). Two-dimensional beings could never know if they live in cylinder version 1 or cylinder version 2 (unless they somehow gained the power to access the unimaginable third dimension).
Cylinder version 2 is called an embedding of cylinder version 1 into three dimensions. The spaces are said to be the same intrinsically, that is, as viewed by 2D beings living inside them.
Next on our menu is the flat 2D torus:
The points of this space are any points in the square I have drawn, including on the edges. We are “gluing” the left and right sides, as we did for the cylinder; we are now also “gluing” the bottom and the top sides.
The flat torus:
- Has an everywhere locally Euclidean geometry. The internal angles of a triangle always add to 180 degrees, and the circumference of a circle is exactly , provided that nothing is wrapping all the way around the torus.
- Has a uniform, or homogeneous, geometry. There is no way for a 2D creature to tell if it is at the middle of the strip, or the left or right edge, or at the top or bottom. (This isn’t obvious; I’ll ask you about this in an exercise.)
- Has zero curvature. Curvature is a local property. (Again, there is a tricky question of how to best think about triangles, or circles, or paths which wrap around the torus in some way. But for the moment I will just worry about local curvature, and the local curvature of the flat torus is always flat.)
- Is closed. It is compact: it is finite in extent. It has no boundary: there is no “edge” to the space.
One more example, before I ask you some questions. The flat torus is given by an abstract “gluing” rule. If we try, in three dimensions, to actually physically glue up the edges of the flat torus as prescribed, the first step goes fine, just as it does for the cylinder:
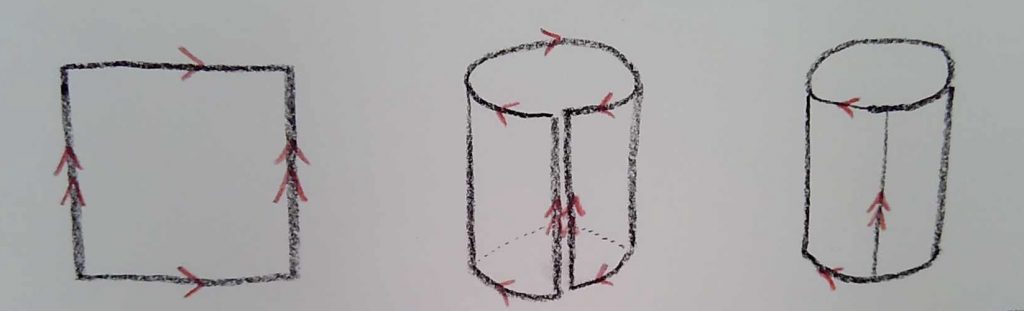
The first, second, and third diagram here are all isometric spaces. I have done no stretching, and certainly no breaking. Pasting the two edges at the last step was just making pairs of points P and P’, which I was supposed to identify anyway, into one point. No problem so far. But now I am supposed to glue together the top and bottom. If you try to do this with paper, you run into trouble. It requires stretching:
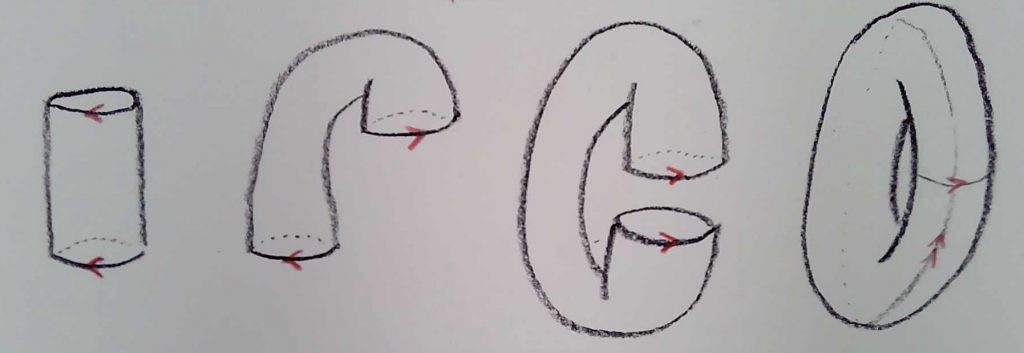
Topologically, this is fine. I have kept the space the same topologically: I have deformed continuously, and not cut or broken anything. But I have changed things geometrically when I stretched.
Let me say that again another way: let’s call the right most diagram in my last picture “torus version 2”. This is the surface of a “donut” shape in three dimensions. From its nature as a surface in three dimensions, I could measure distances on the surface, I could define straight lines (paths of least distance), I could draw triangles etc, all as I did for the sphere. This “torus version 2” has its own geometry, as a surface embedded in three dimensions.
Then “torus version 1” (the flat torus) and “torus version 2” are topologically equivalent, but not geometrically equivalent. In other words, “torus version 2” is a correct topological embedding of the flat torus into three dimensions, but it is not a correct geometrical embedding of the flat torus into three dimensions (it is not an isometric embedding).
OK, before we go further, let me ask you some questions!
Problem 1: Let’s enumerate some of the possibilities:
| Flat | Homogeneous | Smooth | Compact | Has No Boundary | |
| Yes | |||||
| No |
Note that there are potentially 2 x 2 x 2 x 2 x 2 = 32 possibilities here. (I listed “has no boundary” with the odd double-negative, because the “nicer” option is “yes”, there is no boundary. So checking “no” in that column means it has a boundary.)
a) For each of the spaces we have discussed, quickly check off the appropriate yes and no in this table, to check your understanding. (You can just do this mentally.)
b) For every combination of properties that hasn’t already been appeared in the examples we discussed, either make up an example of a space with those properties, or try to explain why that combination is impossible.
Problem 2: I asked this question already on the Slack, but I’ll put it here for reference. Suppose we have a 1 x 1 square, with the edges glued to make a flat torus. Let’s start a line at point A, traveling up and to the right. I want to figure out what the entire infinite line A will look like. (It may not be exactly “infinite”, if it comes back to its starting point.)
a) Suppose the line has slope 2/3. That is, suppose it goes up from point A at (0,0) to meet the point (1,2/3) on the right edge. Figure out what it does after that. Does it meet its starting point? If so, how many times does it go around the torus left to right, and how many times does it go around top to bottom? (You might want to try this using the trick of multiple copies of the square, as I showed in class.)
b) Same question, but with the line having slope 3/4.
c) Same questions, but with the line having slope 7/5.
d) For what slopes will the line come back and meet its starting point? (This is called a closed line, or a closed geodesic.) Are there any slopes for which the line does not come back and meet its starting point? See if you can explain exactly why, in both cases. (I mostly answered this in class, but you should write down the answer in any case to see if you understand it completely; or if you didn’t follow what I said in class, you can try again to figure it out.)
