Hi!

Welcome to the new system!
I’m still figuring out how best to make the online thing work. (Once I figure it out, we’ll be back to in-person anyway!) I think the feedback meetings are valuable, but they were difficult to sustain in this format. So my new plan is to suspend the feedback meetings for now, and to spend time making lectures in this written format.
My hope is that the written format will give you something easier to refer to as you are working through the material. Also, I hope it will make it easier to work on your own. One of the hardest things with the online learning for me has been that it is difficult to have all of you work effectively during class time.
Having the core lecture in written format will free us up to use class time more flexibly, hopefully.
Finally, there is a lot more material I’d like to cover than we will have time for in the term. Writing the lectures will give me more of a chance to make optional side trips, which you can choose to follow based on what interests you.
The story so far
OK, let’s get started! Let me start with a brief recap of where we are so far, and then I’ll explain my plan going forward.
Projections
We opened the class with the problem of projections. This has been the theme for the first half of the class.
To begin with, I imagined that you have a given vector $\vec{v}$ in $\mathbb{R}^3$, and a plane $S$ spanned by two given vectors $\vec{u}_1$ and $\vec{u}_2$, and I asked how to find the perpendicular projection $P\vec{v}$ of $\vec{v}$ onto the plane $S$.
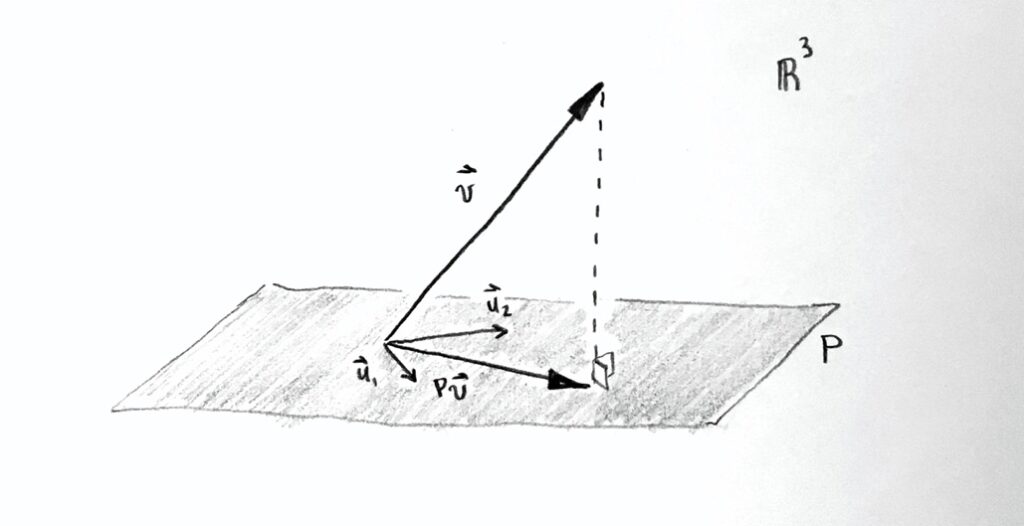
I think this problem has worked out pretty well! Even if you did not get a full solution, I think it helped everyone orient themselves and think about what they knew and what they were trying to do. Also, people came up with several different strategies, all of which we are going to use in various situations!
My intention was that you make an initial to solve this problem with things you knew already. Then I would start the strictly logical development of the theory, and I would use the problem as a motivation for and guide to introducing new theory, which we would use to solve the problem different ways.
So far, this problem has been given two solutions. One way was sketched out in Problem Set 3, Problem #1. It depended on the dot product (or more generally, inner product), which we haven’t formally introduced yet. The second way I discussed in class on Tuesday March 30. The second way required us to find a perpendicular subspace, which I also haven’t formally introduced yet.
In the logical development, I am trying to avoid using the inner product as long as possible. The purpose of this is to make clear what doesn’t depend on the inner product, and what actually needs it. In some applications, we don’t have a natural inner product, or we have more than one.
Least Squares
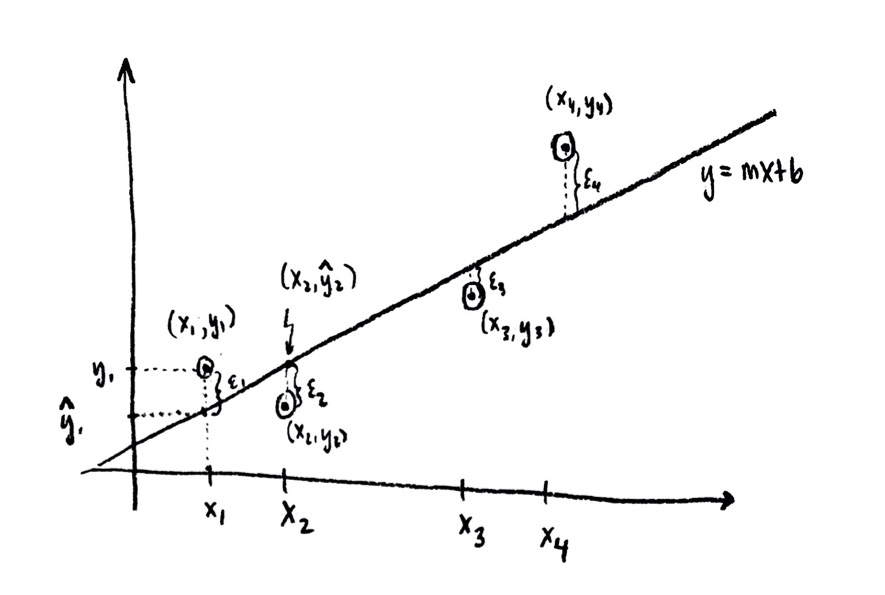
I introduced one major application of projections: “least squares”, which is a way of fitting a line (or curve, or subspace) to some data points in the “best” possible way. This was developed in Problem Sets 1 and 2.
I thought it was important to see a real application early on! Otherwise this all gets too abstract.
Logical Development: Fields, Vector Spaces, Bases, Linear Transformations
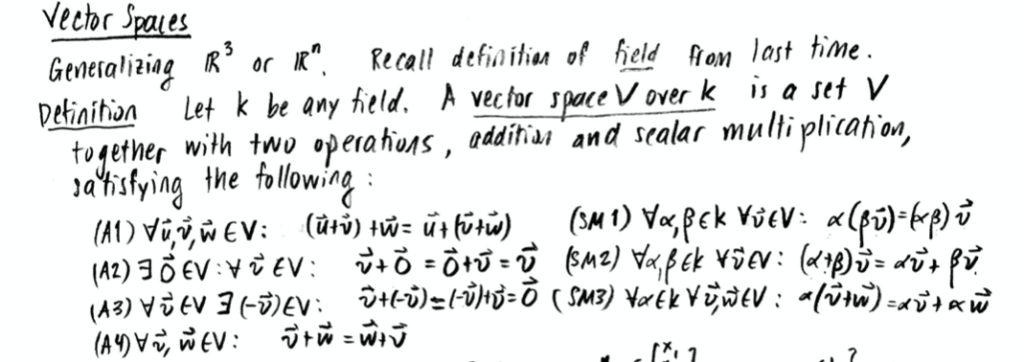
While still thinking about the projection problem, we have then started on the development of the subject in strictly logical order. Logically, it would have made sense to start here, but I was worried that it would be too abstract, and it wouldn’t be clear where it was going. My intention was to give a major practical and theoretical problem (projection), and get you to try it on your own first, so that the general theory would be motivated. But of course the general theory is important for a lot else as well.
Most of Problem Sets 3 and 4 are about the logical development of the fundamental concepts.
A Big Problem For The Second Half: Spectral Decomposition and Decoupling

Just last class (Friday April 2), to start off the second half of the term, I introduced another large motivating problem. Actually, I didn’t quite get there yet: we will get to the main idea and problem in class today (Tuesday April 6).
The plan going forward!
I am introducing the “spectral decomposition and decoupling” problem as a motivation, and I will ask you to spend a bit of time thinking about it, but I am not going to get you to struggle through it on your own, the way I did with the projection problem.
From now on, I want to concentrate mostly on the development in logical order. I will still be splitting between theory and applications, but I’ll bring up the applications when we get to them in logical order. There will be more opportunities now for computational problems, for those of you who are interested in that.
In the written lectures, I will start with reviewing the material we have done so far on fields, vector spaces, bases, and linear transformations, adding some more optional theory and applications along the way. Then I will discuss the projection problems and spectral decomposition problems, and then we’ll move forward to new theory and applications.
Here is the list of topics I hoped to cover in this class. We definitely won’t get to everything, but I’m going to try to briefly touch on all of it, at least in optional lectures and problems. I’ve listed them in logical order, but I may jump out of that order a bit, in order to be sure to get to the most important things.
- Fields (including complex numbers, finite fields, rational field extensions)
- Vector spaces (including function spaces, spaces of polynomials, field extensions, functions on graphs/networks, logical operations, families of subsets)
- Subspaces (things we are projecting to, with examples in all the vector spaces listed above)
- Quotient spaces (optional, but important for theory and for computer graphics)
- Projective spaces
- Linear independence, span, and bases (including Legendre and Hermite polynomials, Lagrange interpolation for curve-fitting)
- Direct sums, complementary subspaces, and projections
- Linear transformations
- Dual spaces
- Basis change
- Gauss-Jordan elimination and systems of linear equations
- Decomposition of projections into tensor products
- Decomposition of linear transformations into tensor products
- Image, kernel, and cokernel
- Parametric and scalar equations
- Error-correcting codes
- Eigenvectors, eigenvalues, and spectral decomposition
- Principal component analysis
- PageRank
- Multilinear functions and tensors; Einstein summation notation
- Inner products
- Quadratic forms
- Orthogonal projection
- QR decomposition
- Singular value decomposition
- Jordan decomposition
- Determinants
- Tensors
- Differential forms
What next?
I will keep posting written lectures. I am planning to start with a recap of the material on fields, vector spaces, bases and linear transformations. I will let you know on the Slack when a new one is posted, and I will list them all on the Advanced Linear Algebra main page.
The written lectures will include problems, which I recommend doing as you work through the lecture, but which I am not asking you to hand in.
I will let you know, on Slack, what are the main things I’d like you to be working on, and what the suggested due dates are for submitting problems.
