Author: admin

Geometry Lecture 1: Angle Sums of Triangles in Cubeworld

In a previous problem set, I asked you what the possible interior angle sums are for triangles in Cubeworld. What is the minimum? What is the maximum?

It seems pretty likely that the minimum is 180 degrees. If a triangle stays on one face, then Cubeworld is exactly Euclidean there. We don’t know how to prove this yet, but it seems pretty solid.

What do the edges do?

Note that the edges don’t actually change the geometry at all. One way to see this is to note that folding a piece of paper does not change any distances measured on the surface of the paper, because paper is not stretchy. So if I draw a straight line–path of shortest distance–from point A to point B on a flat piece of paper:

and then I fold the paper, to make an edge of the cube:

then that path from A to B continues to be a path of shortest distance, since I have not changed any distances. Therefore, I can go back and forth between Euclidean world and “edgeworld” with impunity. The technical name is that there is an “isometry” between the two pictures.

Optional Problem 1: If you find the argument above convincing, you can skip this problem. However, if you find this argument unsatisfying, you can make a more solid argument as follows. Think of the edge as being two flat squares, with a gluing rule: when you leave edge 1, you come out at edge 2 at the same height.

Edge 1 is glued to edge 2.
The gluing is done so that point P is glued to point Q, where P and Q are the same height from the bottom of the square.

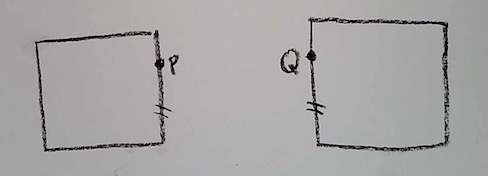
Now, if I have a point A on Face 1, and a point B on Face 2, a Cubeworld straight line between them goes from point A to a point P on Edge 1, which comes out at point Q on Edge 2 and travels to point B. The straight line has to be an ordinary straight line segment on each face (since each face is Euclidean: convince yourself of this!). So the question is, where should point P and Q be, so that the distance AP plus QB is least? Figure out what that placement of P and Q should be, and prove it.

So which triangles have angle sums of 180 degrees?

A triangle that doesn’t contain any vertices can be completely flattened out to a Euclidean one, even if it crosses multiple faces:

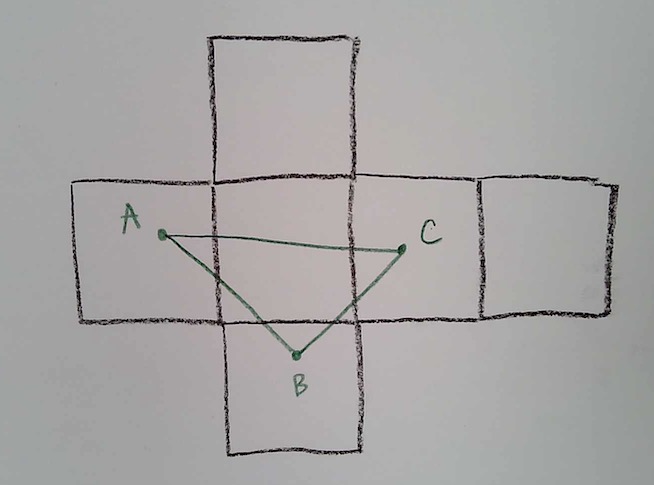
This triangle in Cubeworld will have a 180 degree internal angle sum.

And then it will have a 180 degree angle sum, because it’s a regular Euclidean triangle!

Triangles containing one vertex

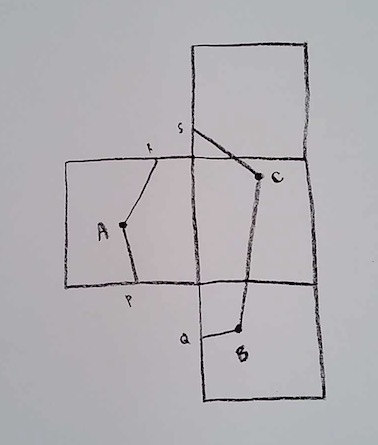
So now, what if a triangle includes one vertex in its interior? You gave examples in class where the angle sum is 270 degrees, e.g.:

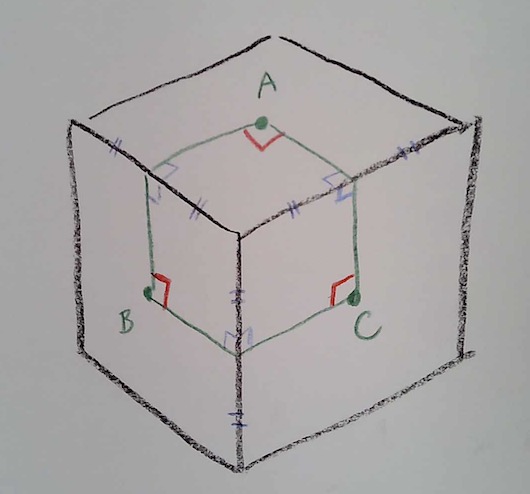
A Cubeoworld triangle. Angles at vertices A, B, and C are each 90 degrees. (This is supposed to be a three-dimensional picture, in perspective.)

Is it always true that a triangle containing one vertex will have a 270 degree angle sum? Many of you were suspecting this, and a few of you gave an argument for it. Let me run through a way of establishing this fairly concretely, which will also be helpful for other Cubeworld questions.

Lines crossing edges again (in more detail)

First, let’s revisit the question of how lines cross edges. Let’s figure out how to draw them in the flattened picture. So, we have a flattened picture of the cube around one vertex V of the cube; let’s just draw the three faces of the cube that meet at that vertex. We have a point A on one face, and a line that leaves A, crosses an edge at point P, and comes out again at point Q on another face. (Points P and Q are the same point when the cube is glued together.)

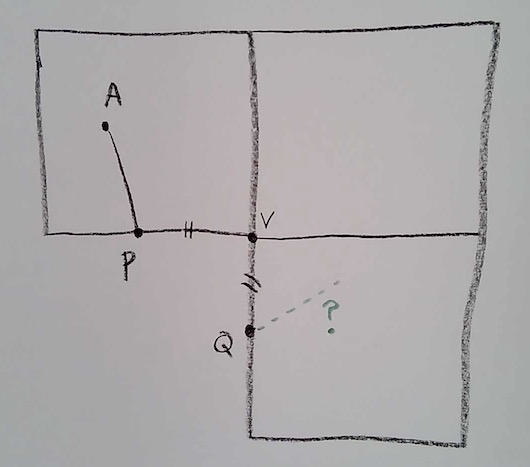
Line segment AP will continue from Q; which way will it go?

To answer this, let’s imagine the point V as a hinge, and let’s swing that bottom face over, so that P and Q meet. In this way, I’m accomplishing the gluing of the edges to make the cube (but I’m cutting another edge).

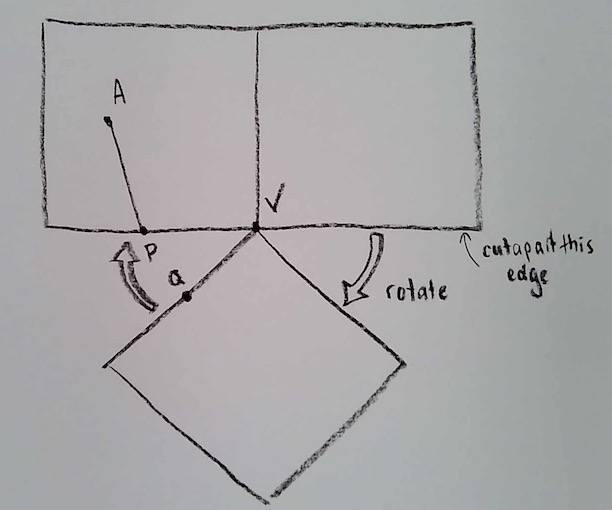
Cut apart the edge on the right side, and rotate the bottom square, hinged at V, so we can glue the edge on the left side, making P and Q meet.

Now that the two sides are glued, so that P and Q meet, it is clear how a straight line should go: the angles should satisfy a=c and b=d.

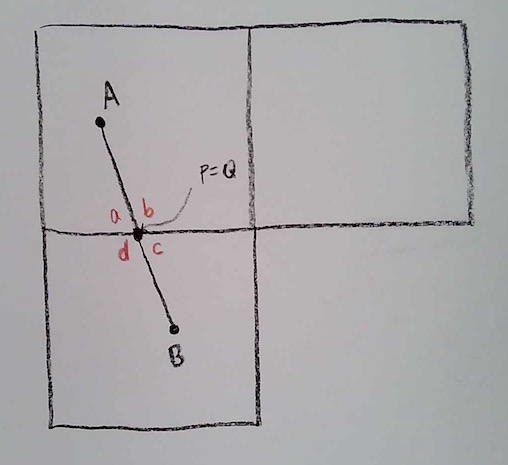
Now that P and Q coincide, we can see that the angles should satisfy a=c and b=d. This tells us what direction the line segment should leave the point Q at as it travels to B.

Now, rotate the bottom face back to its original position, and we get a rule–which looks much less obvious now!–about how the line segment AP should be continued when it comes out at Q:

To continue a straight line segment over an edge, you must make angles a=c and b=d.

Triangles containing one vertex, continued

Ok, now back to a triangle containing one vertex. Let’s take the picture we just drew, and add a third point C, so that ABC is a Cubeworld triangle.

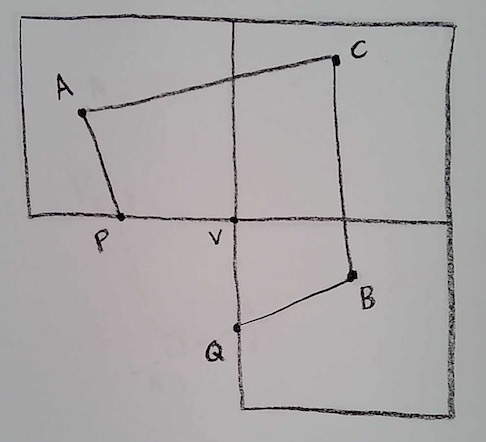
A Cubeworld triangle ABC containing one vertex.

Now, let’s label every angle in sight:

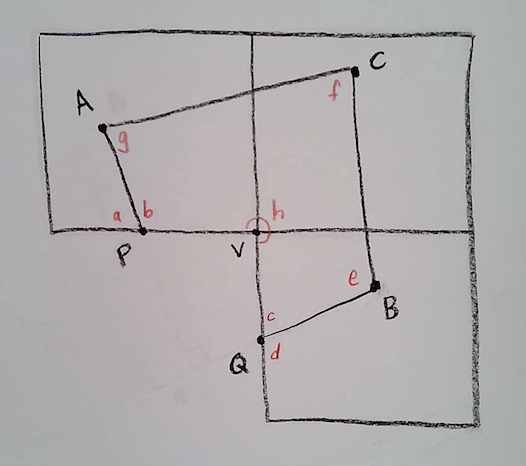
A Cubeworld triangle, containing one vertex, with angles labeled. Note that the internal angle sum of ABC is e+f+g.

The internal angle sum of Cubeworld triangle ABC is e+f+g. We would like to argue that e+f+g is 270 degrees, no matter where we place A, B, and C (provided that the interior of ABC contains vertex V).

Now, notice that we have created an ordinary euclidean 6-gon APVQBC:

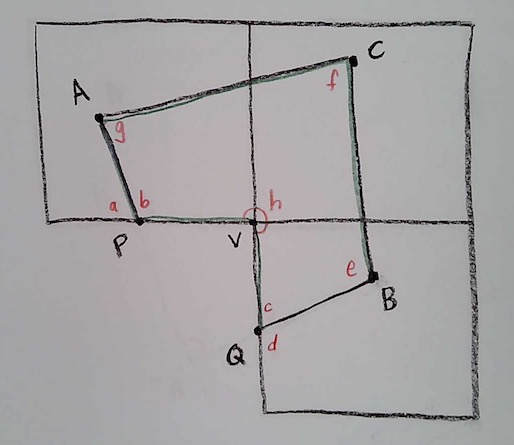
APVQBC is an ordinary Euclidean 6-gon, whose internal angle sum is 720 degrees.

A Euclidean polygon with 6 sides will have an interior angle sum of 720 degrees. I’ll leave it to you to explain why:

Problem 1: Explain why a Euclidean 6-gon will have an internal angle sum of 180 x 4 = 720 degrees.

This means that

e + f + g + b + h + c = 720 degrees.

But now what do we know? We know that h = 270 degrees:

e + f + g + b + 270 + c = 720,
so e + f + g + b + c = 720 – 270,
so e + f + g + b + c = 450 degrees.

We also know that c = a, so we can substitute a for c in our equation:

so e + f + g + b + a = 450 degrees.

But now look at what has happened! We know that b + a = 180 degrees!

e + f + g + 180 = 450
e + f + g = 450 – 180
e + f + g = 270 degrees!

We didn’t assume anything about the placement of A, B, and C, except that V was contained in the interior. So we know that:

Any Cubeworld triangle not containing a vertex in its interior has an interior angle sum of 180 degrees

Any Cubeworld triangle containing one vertex in its interior has an interior angle sum of 270 degrees

Another method

Before we move on, I’d like to show another way of solving this problem, that perhaps some of you would like better.

Let’s say we continue the line segment AP beyond P, into the region which doesn’t correspond to any cube face. Let’s do the same for the line segment BQ. Then, the extended AP and BQ will meet at a new point R (which is not on the cube at all, but is on our flat paper):

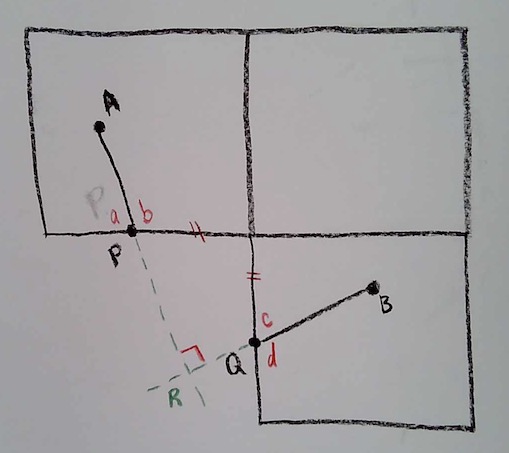
Note that the point R does not correspond to any point on the cube; it is only a point on our flat paper diagram.

Now, by the process described above, when P and Q were meeting, we then took the bottom square and rotated it 90 degrees, to put it back in its original position. Consequently, we have rotated the line BQ by 90 degrees. Before the rotation, BQ and AP lined up; therefore, after the rotation, the extended lines from AP and from BQ ought to be at 90 degrees to each other.

Problem 2: Use this new point R to give an easier proof that
e + f + g = 270 degrees.

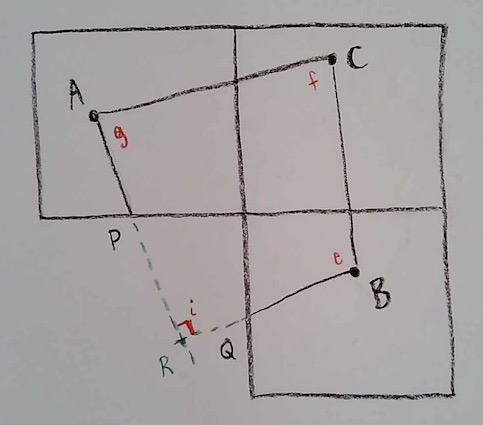
Triangles containing two vertices

Problem 3: Find a Cubeworld triangle that contains two vertices in its interior, if you haven’t already. Try to make it as simple as possible. Find the sum of the interior angles. Does this seem to make sense with what you know already?

Problem 4: Find the angle sum for any Cubeworld triangle that contains two vertices in its interior, if you haven’t already. Make an explanation (proof!) similar to one of the ones I gave for a triangle containing one vertex earlier in this lecture. Your diagram should look something like this:

Triangle ABC contains two vertices of the cube. When the cube is assembled, points P and Q coincide, and points R and S coincide.

Logarithms Lecture 1: Version one: counting the zeroes

In this class, I am going to introduce logarithms multiple times, in multiple different ways. Most of these ways of seeing logarithms have a central property in common:

Logarithms transform multiplication into addition.

I’ll have a lot more to say about this as the course progresses. Keep this in the back of your mind as we start on this first version.

Counting zeroes

This first version is the easiest. The logarithm just counts zeroes. So, the log of the number 1000 is 3, because the number 1000 has 3 zeroes.

We write this:

  • \log(10)=1
  • \log(100)=2
  • \log(1,000)=3
  • \log(10,000)=4
  • \log(100,000)=5
  • \log(1,000,000)=6
  • \log(10,000,000)=7
  • and so on!

And that’s it!

Well, no, not entirely it. There are probably two questions that occur to you at this point. For one thing, what if the number isn’t a nice round number like 1,000,000, but something more like 31,648? And secondly, what is the value of doing such a simple-minded thing in the first place?

I’ll try to start answering the first question now. The second question will be answered gradually throughout the class, but I’ll give a teaser at the end of the post.

How to interpolate log

So, what should the log of a number like 32 be?

There are many different answers you could give to this question. You could say log(32) just isn’t defined: log(10)=1, and log(100)=2, but the number 32 has no zeroes. You could alternately say that the log of every number from 10 up through 99 is equal to 1, and then it jumps to 2 when you get to log(100). So by that reasoning, log(32) would equal 1.

So, there isn’t just one answer to what log(32) should be. But I’m going to try to find an answer that makes the most “sense” (where “sense” is a bit subjective!). This is a question of “interpolation”: how do I fill in the missing values of log continuously?

Log(10)=1 and log(100)=2; what does the graph of y = log x do between those values? How should we connect the dots?

Since log(10)=1 and log(100)=2, and since the logs are getting bigger as the number gets bigger, I’d like to say that log(32) should be a decimal number between 1 and 2.

Moreover, I’d like to say that for all numbers x between 10 and 100, the value of log(x) is between 1 and 2, and that it gets bigger as x gets bigger. So, log (15) should be pretty close to 1, and log(95) should be pretty close to 2. But how do I fill in the numbers exactly?

I could fill them in proportionally. For example, since 55 is halfway between 10 and 100, I could say log(55) should be halfway between 1 and 2. That would mean l0g(55)=1.5. I could figure out other logs similarly. But this procedure ends up not making as much “sense” as I would like. In particular, if I make this definition, I end up getting a graph for log(x) that has straight line segments connected by sharp corners – a sign that something is weird.

Let me try asking a different question: what is a half a zero?

Multiplying numbers adds the zeroes

What would be a number with one and a half zeroes? Would it look something like this?

Well, look at what happens when we multiply multiples of 10. For example, if we multiply 100 x 10,000 we get 1,000,000: two zeroes plus four zeroes equals 6 zeroes. Multiplying the numbers adds the number of zeroes.

So if we multiply a number with one and half zeroes by itself, the two half-zeroes should combine to make a whole zero, and we should get three zeroes in total:

That is, multiplying a number with 1.5 zeroes times a number with 1.5 zeroes should give 3 zeroes total.

Now, what is such a number? It is a number that multiplies by itself to give you 1000? What could that number be? Well, we can start guessing and checking:

  • 30 x 30 = 900
  • 31 x 31 = 961
  • 32 x 32 = 1024
  • 31.5 x 31.5 = 992.25

So, a number with one and a half zeroes is a little bigger than 31.5.

Problem 1: find this number more accurately!

(If you recall your math, this number has a name: it’s the square root of 1000. But it’s instructive to find it by guess and check nevertheless.)

So now we’ve figured out something about logs! Since log(10)=1, and log(100)=2, and since one and a half zeroes is about 31.5, we have concluded that

\log(31.5)\simeq 1.5

Working even more approximately (which I want to do for now), we could say that

\log(30)\simeq 1.5

Another way of saying this: halfway between 10 and 100 is 55 in the additive sense, because

10+45=55, and 55+45=100.

But halfway between 10 and 100 is about 31.5 in the multiplicative sense, because

10 x 3.15= 31.5, and 31.5 x 3.15 = 100.

More roughly speaking, halfway between 10 and 100 is about 30, in the multiplicative sense.

What is this good for?

Before I develop this further, what is the point of this? I’ll try to give a number of different answers in this class. Here’s one which is unfortunately very relevant right now:

By Kenneth Chang, from the New York Times. Link.

In the initial stages of a spreading infection, we expect the number of cases to grow multiplicatively: one person infects two, those two each infect two, those four each infect two… So we expect the number of cases to be multiplied by a certain fixed factor each day. Or said differently, we expect the number of cases to double in a fixed number of days. This is what the phrase exponential growth means.

It is difficult to read rate of growth clearly on a graph when it is exponential: it shoots up too fast. But there is another way of graphing. On the y-axis, we have always been taught to space the labels evenly. That is what happens on the graph at left: each spacing is 15,000 additional cases.

But that is spacing evenly additively. What if we space evenly multiplicatively? Then each marking on the y axis should be a constant multiple of the last one. That’s what is shown on the graph at right: each equally spaced marking on the y axis is 10 times the previous one.

In other words, the y-axis is evenly spaced, counting the number of zeroes: the lines are 1 zero, 2 zeroes, 3 zeroes, etc. In yet other words, the y-axis is showing the logarithm of the number of cases.

On such a graph, an exponential growth is going to be a straight line. (We will see exactly why this is true soon, but hopefully that seems at least plausible to you now.) So we can more easily see deviations from exponential growth. We can see that, as of mid-March, Italy was beginning to succeed at “bending the curve”, whereas the US was not successful at this yet. This is not evident from the graph at left.

I encourage you to read the article I took this graph from. (I believe this article should be free to access, but let me know if not, and I’ll send you a copy.) You can see more detail for different countries at this Financial Times article by Steven Bernard, Cale Tilford, John Burn-Murdoch and Keith Fray.

To connect this to what we started above: if we added more markings to the graph on the right, we would make the multiplicatively evenly spaced. So if we wanted to add an additional marking halfway between 10 and 100, it should be marked about 31.5.

Some questions

Problem 2: What number has a half a zero? In other words, what number x has log(x) = 0.5?
(You can just give an approximate answer.)

Problem 3: Roughly, what is the value of log(3)?

Problem 4: Roughly, what is the value of log(30,000)?
(Hint: Use the fact that 30,000 = 3 x 10,000.)

Please ask questions or discuss, either in the comments here, or on our Slack channel!

css.php