(Problem Set #7)
Hi again! If you’ve worked through the lecture on Volumes of Spheres, then you’ll be ready to try some similar problems. The first problem, which I’d like everyone to work through and write up, is the problem I put at the end of that lecture, to find the volume of a square-based pyramid. I’ll repeat it here for reference:
Problem: Volume of a square-based pyramid.
Suppose that I have a pyramid with a square base. That is, I start with a square horizontal base, and then I choose a point vertically directly above the center of the square. I connect the top point to the four corners of the square with line segments, then I fill in the four triangles I have created, and finally I fill in the resulting solid.

Let’s say the height is and the base is .
a) First, before you get started, make a guess about the formula. Try putting the pyramid in a box: what’s the volume of the box? What fraction of the box do you think the pyramid will take up?
b) Then, follow all the steps I did for the sphere, one by one, with the pyramid. At each step, pay attention to what is the same, and to what you need to change.
c) Once you get an answer (it may take a while!), test it out the way I did with the sphere. Does your final answer agree with your guess?
Since that problem is the first exercise, I (or Džen) will be very generous with hints and suggestions, just ask!
Once you’ve completed that problem, you could either do some quite similar problems, or if you are feeling confident, you could try a more challenging problem. There are more problems here than you will probably have time for, so you can pick and choose.
Fairly similar volume problems
Here are two volume problems which are pretty similar to the sphere and the square-based pyramid, if you’d like to try similar things to build your understanding and confidence with this method. You could do both, or choose one (doesn’t matter which). Or, if you are feeling confident, you could skip ahead to other problems.
Problem: Volume of Right Circular Cone
A “right circular cone” is the shape you get as follows: start with a circle $C$ on the ground. The base of the cone is the filled-in circle of all the points on the ground inside the circle. Pick a point $P$ that is directly above the center point of the circle $C$. For each point $q$ on the circle $C$, make a line segment from $q$ to $P$; the (infinitely many) line segments you get form the curved side surface of the cone.
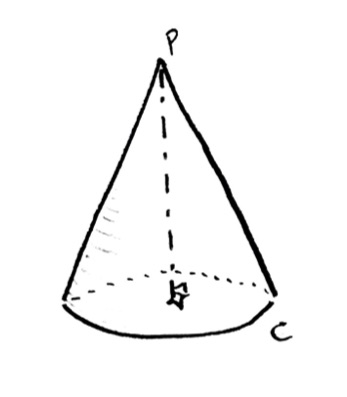
The solid cone is all the space that is contained above the base circle, and under the curved sides with top point $P$. Find the volume of the cone! (Your answer will be in terms of the dimensions of the cone, in some way: you choose what dimensions are appropriate!)
Here’s another similar one:
Problem: Parabolic Bowl
Suppose that we start with the graph of the parabola $y=x^2$, in an $x$-$y$ plane (I want to imagine that the $y$ axis is vertical). Let $h$ be some positive constant. I want to start with the region that is above the curve $y=x^2$, below the line $y=h$, and to the right of the $y$-axis:
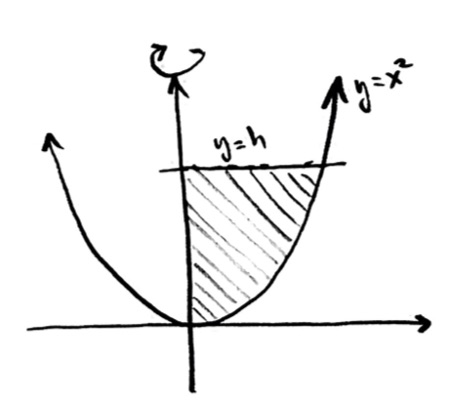
Then, I imagine rotating that region $360^\circ$ around the $y$-axis, keeping the $y$-axis as a fixed line (axis of rotation). The space that shaded region sweeps out in space has the shape of a solid parabolic “bowl” or “bullet”:
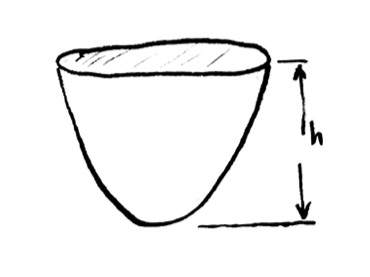
Find the volume of this parabolic bowl!
Areas
A very similar method works for finding areas. You imagine gradually filling in the area, up to some “depth” (or it could be “width”, or other parameter). In this case you are finding $\mathrm{d} A$ rather than $\mathrm{d} V$, but the method is otherwise similar. If you haven’t taken calculus before, I’d definitely recommend trying this problem. If you have, you’ve probably seen problems like this frequently, so you might want to skip it—up to you!
Problem: Parabolic Area
Suppose that we start with the graph of the parabola $y=x^2$, in an $x$-$y$ plane. Let $h$ be some positive constant. I want to consider the region that is above the curve $y=x^2$, below the line $y=h$, and to the right of the $y$-axis:

Find the area of the shaded region!
Generalization!
If you’d like to try something a little more challenging, and want to see some interesting more general rules following from the above, try these two problems.
Problem: Volume of Slant Pyramid
In the “Volume of Square-Based Pyramid” problem at the top, I assumed that the top corner (let’s call it $P$) was directly above the center of the base square. What if I didn’t do that? Let’s define a “slant pyramid” as follows: first, make a horizontal square $S$ on the ground. All the points enclosed within the square on the ground will form the base. Now, pick $P$ to be any point above the ground. Form four edges by connecting each of the four corners of the square $S$ with the point $P$. This creates four triangular faces. The “slant pyramid” is the solid contained by the square base and the four triangular side faces.
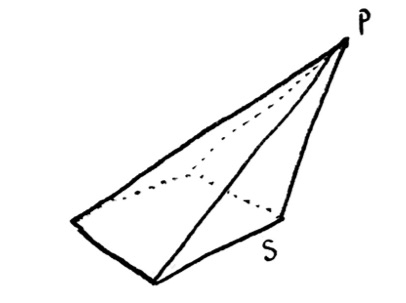
What is the volume of the slant pyramid? (Your answer will involve the dimensions of the slant pyramid somehow. Use whatever specification of the dimensions that you think makes the most sense.)
That generalization is actually a special case of the following generalization:
Problem: Volume of Any Cone
You may have noticed that my definition of a “right circular cone” would work to define a square-based pyramid also—just replace the circle base $C$ with the square base $S$, and leave the rest of the definition the same. More generally, we could do the same with a triangle base, or a pentagon base, or an ellipse base. . .
We define a “cone with arbitrary base” as follows. Let $C$ be any closed curve, in a horizontal plane, that doesn’t intersect itself. The base will be all the points on the horizontal plane which are contained within $C$. Pick any point $P$ above the horizontal plane. For each point $Q$ on the curve $C$, form the line segment connecting $Q$ to $P$. The (infinite) family of line segments created form the sides of the cone. The solid cone is all the points in space enclosed by the base and the sides.
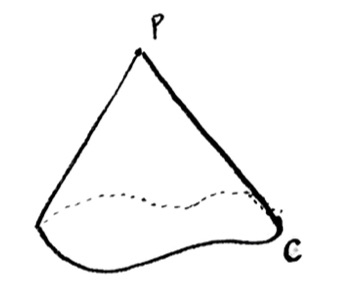
Let’s say the area of the base is $A$. Find the volume of this cone. Your answer will involve $A$, and also at least one other dimension of the cone (which you can choose).
An area challenge
If you are looking for a challenge, you might try this problem. It is definitely doable with everything we have done so far—the only extra thing is you need to remember a little bit of trigonometry. It is a challenge which also involves some ideas which will be useful if you go further with calculus or physics.
Problem: Area of a Sphere
In a previous problem, we have shown how to find the formula for the surface area of a sphere of radius $r$, assuming that the volume formula was already known. (Remind yourself which question, and what the answer was!!) It is possible to find the surface area of a sphere of radius $r$ more directly, using the sorts of ideas that we have been developing above. Try it! (If you can’t get a complete answer, at least write out your strategy, and ask for hints! The ideas are important and interesting, even if you don’t get a full answer.)
Some volume challenges
Here are two problems that are interesting, if you are looking for a challenge with computing volumes!
Problem: Volume of a Torus
Suppose $r$ and $R$ are two positive constants, with $r<R$. Suppose we draw a circle $C$ in an $x$-$y$ plane, with radius $r$, and whose center is at the point $(R,0)$. Now, imagine that $y$ is vertical, and rotate this circle $360^\circ$ around the $y$-axis, keeping the $y$-axis fixed (axis of rotation). The resulting surface is called a “torus”:

The solid torus is the region of space enclosed by the torus surface. Find the volume of the solid torus!
This last one is super challenging:
Problem: Volumes of Platonic Solids
The “Platonic solids” are the analogue of regular polygons in three dimensions. Unlike regular polygons, there are only finitely many of them—in fact, only five:
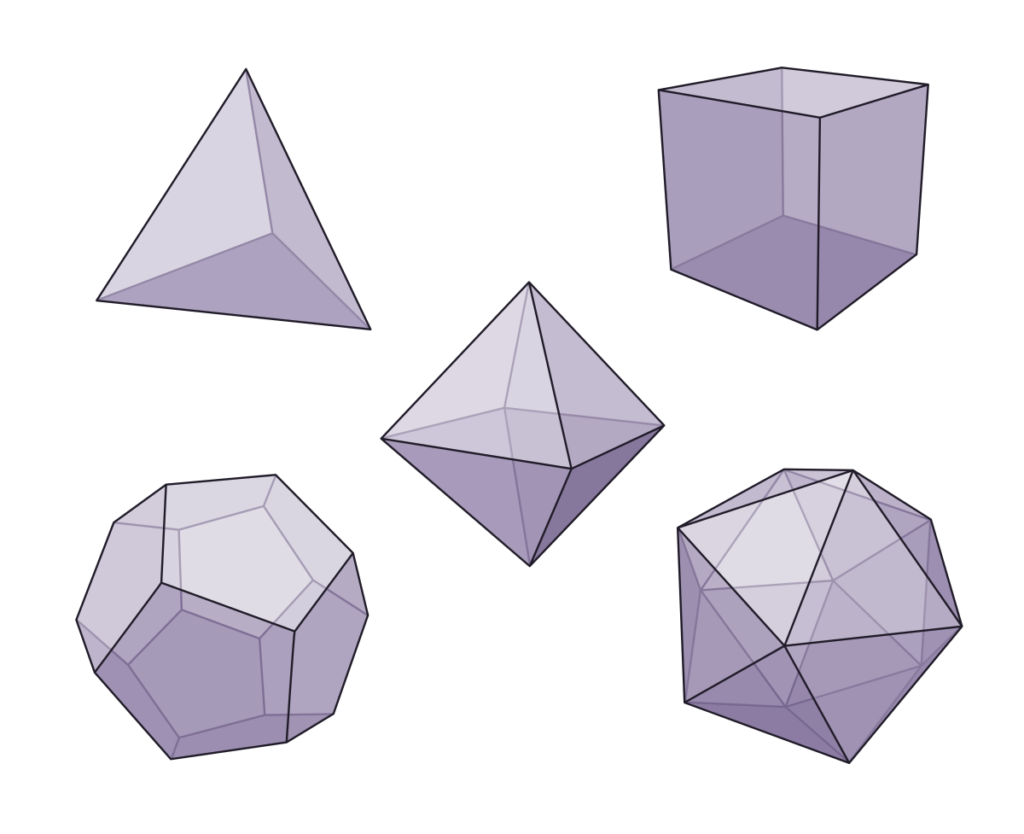
See Wikipedia for more information. What are the volumes of the Platonic solids, as formulas of their side lengths? One is easy (!), and two of them are not hard given the things you have figured out in previous problems. The remaining two are doable with things you have already figured out, but geometrically tricky!
