
Hi!
In the lecture on Volumes of Spheres, at the end, I asked you to try doing the volume of a square-based right pyramid, the same way that I did the sphere. Let me repeat the question again for reference:
Problem: Suppose that I have a pyramid with a square base. That is, I start with a square horizontal base, and then I choose a point vertically directly above the center of the square. I connect the top point to the four corners of the square with line segments, then I fill in the four triangles I have created, and finally I fill in the resulting solid.

Let’s say the height is $h$ and the base is $b$.
a) First, before you get started, make a guess about the formula. Try putting the pyramid in a box: what’s the volume of the box? What fraction of the box do you think the pyramid will take up?
b) Then, follow all the steps I did for the sphere, one by one, with the pyramid. At each step, pay attention to what is the same, and to what you need to change.
c) Once you get an answer (it may take a while!), test it out the way I did with the sphere. Does your final answer agree with your guess?
I will write out the solution in full here. Please do try the solution yourself first, following the same pattern as what I did with the sphere. If you got stuck somewhere, I would suggest looking at this solution until you get a hint for the place that you were stuck, then try it yourself again from there.
Get an initial guess or estimate
It isn’t strictly logically necessary, but it is almost always helpful to get a rough idea of the answer before you begin solving.
For this problem, I need to find the volume of a pyramid, which I don’t know. (If you do know it, pretend you don’t for now!) What do I know volumes of? I know the volume of a sphere, but that doesn’t seem helpful. The only other thing I know is a box: a right-angled rectangular box of dimensions $\ell$, $w$, and $h$, has volume $V=\ell w h$.
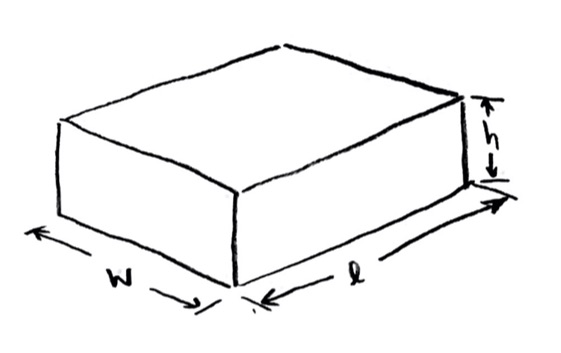
(That’s pretty much by definition; when we define what volume means, we usually start there. Actually, you derive this from a simpler assumption, but it’s a little off-topic; I’ll post something on it if anyone is interested.)
Anyway, we could compare the volume of a pyramid to the volume of a box:

The smallest box that I can put the pyramid in has dimensions $b$, $b$, and $h$; so the volume of the pyramid has to be less than $V_{\mathrm{box}}=b^2h$.
In fact, it would be reasonable to guess (wouldn’t it?) that the pyramid takes up some fixed fraction of the box. That is, if I changed $b$ or $h$, that the relation of the volume of the pyramid to that of the box would stay the same. That would mean that the volume of the pyramid should be of the form
$V=cb^2h$,
where $c$ is some constant number less than 1.
Looking at the picture, and thinking about the missing space, it seems that the pyramid takes up less than half of the box. So I would further guess that $c$ is a number less than 1/2.
Now, I certainly haven’t clearly proved this is true. But I’m just getting initial guesses, so I won’t try harder to justify it now. (It could potentially be interesting to do so later though.)
I could get a lower estimate on the volume of the pyramid by placing a rectangular box inside the pyramid. That seems like something I could figure out, but it might take a little doing. So I won’t get sidetracked now, since I was just trying to get a rough guess anyway.
OK, so our guess for the volume of the pyramid is
$V=cb^2h$,
where $c$ is some constant number less than 1, and probably less than 1/2.
Now on to the method!
Changing to dynamic: filling up gradually
Following the method I showed for the sphere, our first step will be to replace the problem of finding the fixed volume of the given pyramid, to finding the changing volume of the partially-filled pyramid, as I fill it up gradually.
I imagine that the pyramid is a tank filling with water. I fill it up to a depth $z$, where $z$ is less than or equal to the total height $h$ of the pyramid.
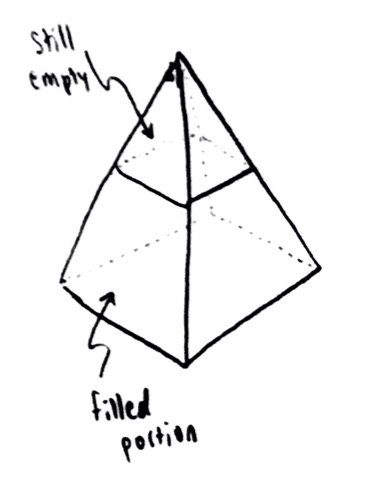
From a side cross-section, it looks like this:
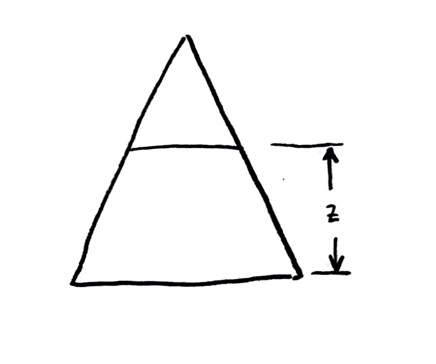
Now, I am looking for the volume $V$ of the filled section only. This means that $V$ is a function of $z$; as $z$ increases, so does $V$.
(The function $V$ also depends on $b$ and $h$, but I am thinking of these as constant, since the dimensions of the pyramid do not change when I am doing this problem.)
Letting filling parameter increase slightly
The next step was to see what happens when I add just a little more water. In this problem, the parameter that controls how full the pyramid is, is the depth of the water $z$. So imagine that I start filled to some depth $z$, and then I fill a little more, so $z$ increases to $z+\mathrm{d}z$. Then the volume also increases, from a value $V$ (when the depth was $z$) to a value $V+\mathrm{d}V$ (when the depth is $z+\mathrm{d}z$).
This looks something like:
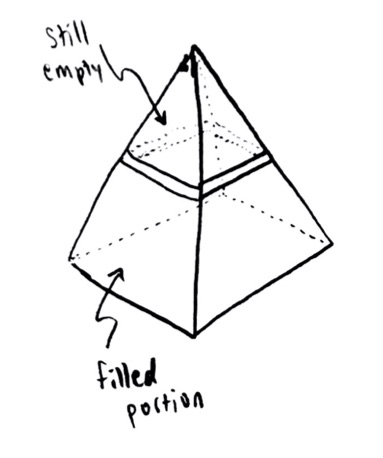
From the side, it looks like

I want to find out the increase in volume, $\mathrm{d}V$, in terms of the other variables and constants.
The shape of the extra volume is approximately a square plate! Let’s give a name to the length and width of the square plate; I’ll call them $x$ and $y$. But because the base is square, the slice is also square, so $y=x$.

The extra volume $\mathrm{d}V$ we have added is
$\mathrm{d}V= x y \,\mathrm{d}z = x^2\,\mathrm{d}z$.
Success!
(It’s not exactly true! The sides of the little extra slice are not perpendicular to the base, so it’s not truly a right-angled rectangular box. However, the error we are making is going to be proportional to $(\mathrm{d}z)^2$, so for “infinitely small” $\mathrm{d}z$ it disappears. More precisely, the error we have made will contribute an error to our final answer, but because it is proportional to $(\mathrm{d}z)^2$, the error approaches zero as we take the limit of $\mathrm{d}z$ approaching zero.)
Note that the $x$ gets smaller as $z$ gets bigger, so the volume of the slice $\mathrm{d}V$ that we are adding is relatively big if $z$ is small, and gets smaller as $z$ gets larger. Which makes sense with the diagram (right?).
I could divide both sides of my equation above by $\mathrm{d}z$, to find
$\dfrac{\mathrm{d}V}{\mathrm{d}z}=x^2$.
A warning: writing dV in terms of the filling parameter only
Now, I might be tempted at this point to say, I know the derivative $\frac{\mathrm{d}V}{\mathrm{d}z}$ of the function $V$ I’m looking for. Then I would say, the derivative is $x^2$, so $V=\frac{1}{3}x^3+C$, and done, right?
That does NOT work. The reason is that I have found the derivative of $V$, assuming that $z$ is the variable. The quantity $x$ is a variable, which depends on $z$. We could think of $x$ as standing for an unknown formula of $z$. So the derivative of $V$ isn’t truly $x^2$; instead, it is some unknown formula of $z$, all squared.
So, to proceed further, we have to find exactly how $x$ depends on $z$.
Finding x in terms of z
Our goal is now to find exactly how $x$ depends on $z$. Once we do that, we can get a formula for $\frac{\mathrm{d}V}{\mathrm{d}z}$ that depends only on $z$.
Now we’ve got to do some geometry. Take a look at that cross-section, and start labeling everything you know:
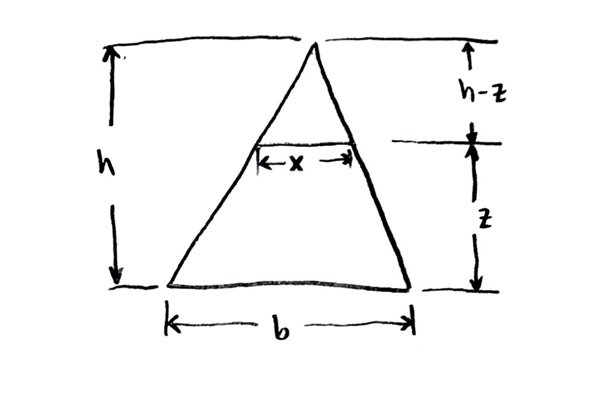
Note that I figured out one thing on the diagram that wasn’t given: the height of the little empty triangle on top must be $h-z$, the total height of the pyramid minus the height of the filled portion.
Now, we have a proportional (or similar) triangles question! The little triangle at the top is just a scaled version of the entire large triangle:
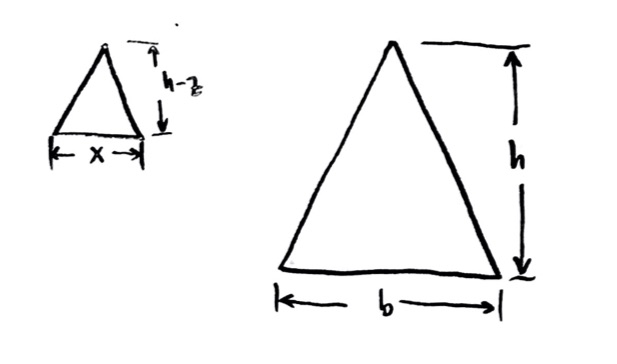
I’m trying to find $x$, so let me arrange a fraction where it is on the top. We could say
$\dfrac{x}{h-z} = \dfrac{b}{h}$;
that is, the proportion of base to height must be the same for both triangles. That’s usually the way I think of it. Some people prefer to think of it as
$\dfrac{x}{b}=\dfrac{h-z}{h}$;
what that says is, whatever proportion the first base is of the second base, the proportion of the first height to the second height should be the same value. (Like, if $x$ is, say, 1/4 of $b$, then the height $h-z$ should also be 1/4 of $h$.)
You can think of it either way you like. Both will give you the same equation in the end.
I’m trying to find how $x$ depends on $z$, so I want to solve for $x$. Starting with either equation above, I get
$x=\dfrac{b}{h}(h-z)$.
It’s always a little subjective what counts as “simplified”, and you might want to multiply through this bracket. I’m going to leave it the way it is for now, because I know I want to find $x^2$ soon.
Finding dV/dz in terms of z only (and constants)
OK, so the purpose of this was to find $\mathrm{d}V$, and $\frac{\mathrm{d}V}{\mathrm{d}z}$, in terms of z only. So let’s substitute our formula for $x$ in terms of $z$, into our formula for $\frac{\mathrm{d}V}{\mathrm{d}z}$. We get
$\dfrac{\mathrm{d}V}{\mathrm{d}z}=x^2=\left(\dfrac{b}{h}(h-z)\right)^2=\left(\dfrac{b}{h}\right)^2(h-z)^2=\dfrac{b^2}{h^2}(h-z)^2$.
Now, once again, “simplified” is a little bit subjective here. This is a nice simple answer. But, I’m going to want to find the antiderivative of this function shortly. And having that parenthesis squared is going to cause me problems. My life will be easier if I multiply the thing out:
$\dfrac{\mathrm{d}V}{\mathrm{d}z}=\dfrac{b^2}{h^2}(h-z)^2=\dfrac{b^2}{h^2}(h^2-2hz+z^2)=\dfrac{b^2}{h^2}h^2-2\dfrac{b^2}{h^2}hz+\dfrac{b^2}{h^2}z^2$.
Simplifying the fractions, I get finally that
$\dfrac{\mathrm{d}V}{\mathrm{d}z}=b^2-2\dfrac{b^2}{h}z+\dfrac{b^2}{h^2}z^2$.
This formula truly gives me the derivative of my unknown function $V$ with respect to $z$—with no surprises—because it depends only on the variable $z$. It also depends on $h$ and $b$, of course, but for the purposes of this problem, those are constants—we can think of them as being fixed numbers.
This formula tells me how the the partially filled volume $V$, that is, the volume of the water, changes as the depth $z$ changes.
Now we’re getting close!
Finding the antiderivative
We know the derivative of the function we’re looking for! So we have to reach back to problem set 1, and the rules we had for derivatives. Finding the antiderivative is a sort of guess-and-check: what function would give me the derivative that I want?
Our formula for $\frac{\mathrm{d}V}{\mathrm{d}z}$ has three terms. Let’s tackle it one term at a time.
First, $b^2$. A warning: the antiderivative is NOT $\frac{1}{3}b^3$! Remember that $b$ is a constant here, just a number. So $b^2$ is equally well a constant. It’s as if we were given something like $\frac{\mathrm{d}V}{\mathrm{d}z}=7$; then $V$ could have been $7z$.
So, the antiderivative of $b^2$, with $z$ as a variable, is just
$b^2 z$.
(Plus an added constant, but I’ll leave those to the end.)
Second, $-2\frac{b^2}{h}z$. Again, the forbidding-looking expression $-2\dfrac{b^2}{h}$ is just a constant. So, it’s just as if we were given something like $\frac{\mathrm{d}V}{\mathrm{d}z}=7z$. If the derivative has a $z$ to the power 1, then then original power had to have been 2. We can’t make $V=7z^2$, though, because then we would get $\frac{\mathrm{d}V}{\mathrm{d}z}=14z$ instead. We need to introduce a factor $1/2$, to cancel the 2 we get when we take the derivative of $z^2$. So, the antiderivative of $7z$ would be $7\left(\frac{1]{2}z^2\right)=\frac{7}{2}z^2$.
Similarly, the antiderivative of $-2\frac{b^2}{h}z$ is going to be
$-\dfrac{b^2}{h}z^2$.
Third, $\dfrac{b^2}{h^2}z^2$. As before, the fraction in front is just a constant. The antiderivative of $z^2$ has to have a power 3, and we have to cancel the 3 that is created when we take the derivative. So, the antiderivative of $z^2$ is $\frac{1}{3}z^3$.
This means that the antiderivative of $\dfrac{b^2}{h^2}z^2$ is
$\dfrac{1}{3}\dfrac{b^2}{h^2}z^3$.
Putting it all together, the antiderivative of
$\dfrac{\mathrm{d}V}{\mathrm{d}z}=b^2-2\dfrac{b^2}{h}z+\dfrac{b^2}{h^2}z^2$
is
$V=b^2 z-\dfrac{b^2}{h}z^2+\dfrac{1}{3}\dfrac{b^2}{h^2}z^3+C$,
where C is an unknown constant.
Evaluating the constant
Before we first start filling up the pyramidal tank, the height of the water starts at $z=0$. At that time, the volume filled so far is $V=0$. Putting both of those into our formula for $V$ given above, we find
$0=b^2(0)-\dfrac{b^2}{h}(0)^2+\dfrac{1}{3}\dfrac{b^2}{h^2}(0)^3+C$,
which all just boils down to
$C=0$.
Therefore, the formula for the volume, of the pyramid filled up to a depth $z$, is given by
$V=b^2 z-\dfrac{b^2}{h}z^2+\dfrac{1}{3}\dfrac{b^2}{h^2}z^3$.
Awesome!
Filling the whole volume to get the final answer
My original problem was to find the entire volume of the pyramid. I introduced this idea of filling it to a depth $z$ as a device. So, to answer the original problem, I should set the depth $z$ to be the whole height of the pyramid, so that the entire thing is filled up:
set $z=h$!
Doing this in our formula for the volume $V$ of the partially-filled pyramid, we get a lot of simplification:
$V=b^2 (h)-\dfrac{b^2}{h}h^2+\dfrac{1}{3}\dfrac{b^2}{h^2}h^3=b^2h – b^2h +\dfrac{1}{3}b^2h=\dfrac{1}{3}b^2h$,
so our final answer is
$V=\dfrac{1}{3}b^2h$.
Hooray!
Verifying the answer
Let’s see what checks we can put this answer through. First off, we had guessed that the volume of the pyramid would be
$V=cb^2h$,
where $c$ is some positive constant that is less than 1, and probably less than 1/2. In fact, our final answer exactly fits this guess, with $c=1/3$. Beautiful!
That’s pretty strong evidence that it’s right, I think.
What else could we do? One thing I notice is that the partially filled pyramid is actually a big pyramid minus a small pyramid on top. If our formula is correct, then the big pyramid has volume
$V=\dfrac{1}{3}b^2h$
and the smaller pyramid on top has volume
$V=\dfrac{1}{3}x^2(h-z)=\dfrac{1}{3}\left(\dfrac{b}{h}(h-z)\right)^2(h-z)=\dfrac{1}{3}\dfrac{b^2}{h^2}(h-z)^3$.
So, the volume of the partially-filled pyramid (up to a depth $z$) should be
$V=\dfrac{1}{3}b^2h-\dfrac{1}{3}\dfrac{b^2}{h^2}(h-z)^3$
Does this agree with the formula we got above,
$V=b^2 z-\dfrac{b^2}{h}z^2+\dfrac{1}{3}\dfrac{b^2}{h^2}z^3$?
Bulldozering through the algebra, it does seem to match!
That’s probably a little bit logically circular, maybe. But I’m not trying to get a proof here, I’m just trying to run consistency checks. Our formula checks out!
Looking back: could we simplify?
It’s always a good idea to look back on a solution—particularly a long one—and try to summarize, clean up, and see if you could have done things more easily. It’s also good to look for lessons for next time.
One thing which would make things easier, which at least one of you noticed already: I could have flipped the pyramid over, and filled it from the tip. Or alternately, I could have filled the pyramid from the top down (antigravity water??).
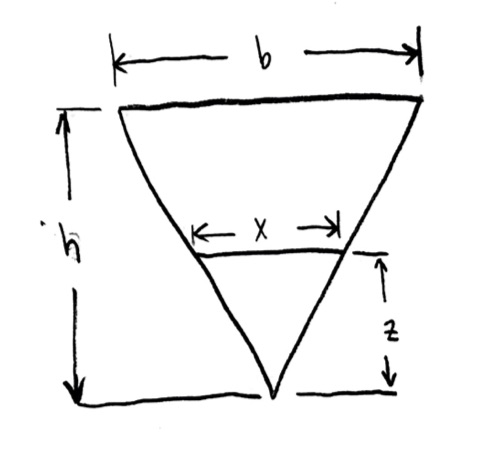
Then the algebra of my proportional triangles becomes a lot easier. And as a result, my antiderivatives come out a lot easier as well.
Exercise:
Do the problem the way I just described, putting the pyramid upside-down first. (Or you can leave it right-side-up, but just fill it from the top down.) You don’t have to write the whole problem again, just write out the parts that are different. It should come out a fair bit easier!
It’s also worthwhile to see if you can solve other similar problems the same way. One thing that is clear is, the base could have been a rectangle instead of a square, and things wouldn’t change too much.
Exercise:
Do the problem again, assuming that the base is a rectangle with length $\ell$ and width $w$. Again, you don’t have to write out the whole thing: just identify what changes. You could probably make a guess how the answer should come out, and then check it.
Another thing that could be generalized: it didn’t seem to matter too much that the tip of the pyramid was directly over the base.
Exercise:
Suppose that we have a rectangle-based pyramid, with base length $\ell$ and width $w$, and with perpendicular height $h$; but let’s assume that the top point of the pyramid is directly above one of the corners of the rectangle. (So the pyramid is kind of a 3-D version of a right-angled triangle.) Go through your solution, and figure out what step needs to change, and how the final answer would change (if indeed it does).
I ask some similar problems in the “Generalization” part of Problem Set 7, Problems on volumes and areas.
