Hi there!
Hi there!

I hope those of you who are on campus are enjoying the pleasant weather.
I am going to try something a little different for Calculus, starting here. I am going to write my lectures, in a fairly conversational form. As I write the lecture, I’m going to stop and ask you to try things on your own. This is where, in a classroom, I would actually stop and wait for you to try it out. Written, it’s awfully tempting to charge ahead, and heck, I can’t stop you. But let me recommend stopping at those points and working things through on your own: what follows will make more sense if you’ve thought it through yourself first (and it’s awfully satisfying to successfully anticipate where I am going).
I’m not asking you to hand in these problems embedded in the lecture, but you can if you like as evidence of your work! I will also be repeating some of them in problem sets.
By putting the straight lecture parts of the class in this written form, I’m hoping that the Zoom classes can then be more about discussion, questions, and work.
Volume of a sphere: why?
This first lecture will be about the problem of finding the volume of a sphere. I asked you about this on Problem Set 6, Problems #3 and 4. What I’m going to do is walk you through my thinking on this problem. If you work through this lecture, you’ll have a solution to those problems (and I’ll take it a little further).
OK, to start, what am I trying to find? I imagine that I have a solid round ball, of some known radius (let’s call it $r$). Like, imagine a basketball. A regulation basketball has a radius of approximately 12cm. What proportion would it take of a cubical box? How many 1cm sugar cubes would fit in it? (We’re allowed to cut the cubes into pieces around the edges to fit more neatly.) If we put it in water, how much volume of water would it displace?

Honestly, nobody actually cares about the volumes of basketballs that much. You may care about basketballs a great deal, but why would you ever want to know the volume? What would that be good for? I only mention basketballs to make something you can easily picture. However, if we are talking about a spherical planet, or star, or water droplet, or (approximately) atomic nucleus, then we may have good reasons to want to know the volume.
More than that, this is a question of mathematical curiosity. We know the formula for area of a circle (at least, we’ve been told the formula, and we’re thinking about it more in this class!). So we ought to be able to find the formula for the volume of a sphere, right? Could it be as simple as $\pi r^3$? If it’s not, then why? (You may remember a formula for the volume of a sphere, but where does that come from?)
More importantly, the technique I want to show you here works for all kinds of other problems: volumes and areas of different shapes, sure, but also an enormous set of other problems. It is a key idea in calculus.
Ok, let’s get started on finding the volume of a sphere!
Getting started: drawing a diagram
Since it’s hard to draw in three dimensions, let’s start by drawing a cross-section of the sphere from the side:

Well, admittedly, that is not a very impressive diagram.
I have imagined taking a cross-section through the center of the sphere (cutting it in half), and viewing it from the side. One important piece of information is that this means the circle I have drawn has the same radius $r$ as the sphere does. (Right?)
Out of habit, I could draw my diagram on coordinate axes. Since this is three-dimensional, I might use an xyz axis system, where the z-axis points up. Then my diagram would look like this:
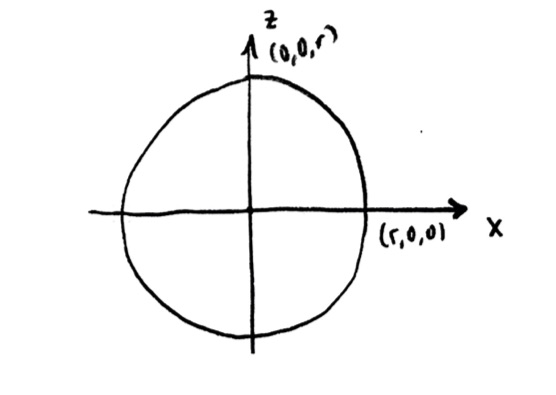
I’ve assumed that I took the cross-section along the x-axis. By making a cross-section and viewing from the side, I’m avoiding making a more difficult 3-D drawing. The y-axis doesn’t appear here, because it is pointing directly away from us.
I don’t know if drawing the coordinates will help, but it’s worth a try.
Simplifying slightly by symmetry
It’s often a good idea to use a symmetry of your problem. In this case, the volume of the lower half of the sphere will equal the upper half of the sphere. So we could just find the volume of the upper half, then multiply our final answer by two:
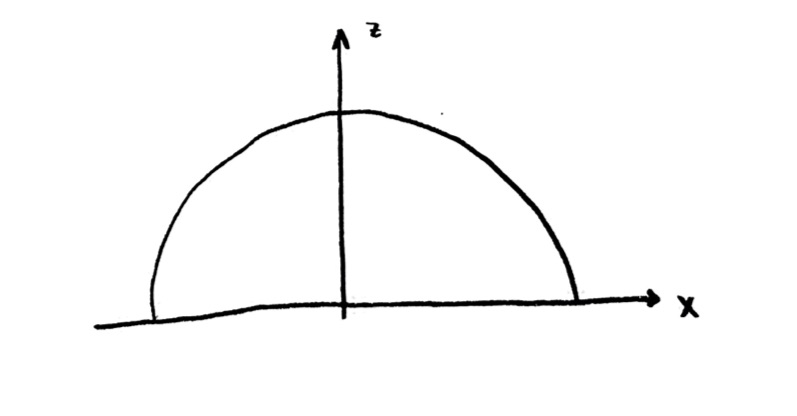
I’m not certain this will be easier, but it might be! It might at least be nice that we only have to deal with positive z values. Let’s try it.
The dramatic clever step!!
This is the key step!! We are going to replace the problem with a seemingly harder problem. Let’s imagine that the half-sphere is a hollow tank (whose walls are very thin) that we are filling with water. So I want to find the total volume of water when the tank is full. I’m going to replace this with the harder problem of finding the volume of water when the tank is not completely full!
So, suppose that the half-sphere is a hollow tank. Let’s fill it partially with water, to some height less than the height of the tank. Let’s make up a name for the height: I’m going to call it $z$, since it’s a coordinate on the z-axis, (but I could have equally well called it $h$, or anything else). Then my side cross-section view looks like this:
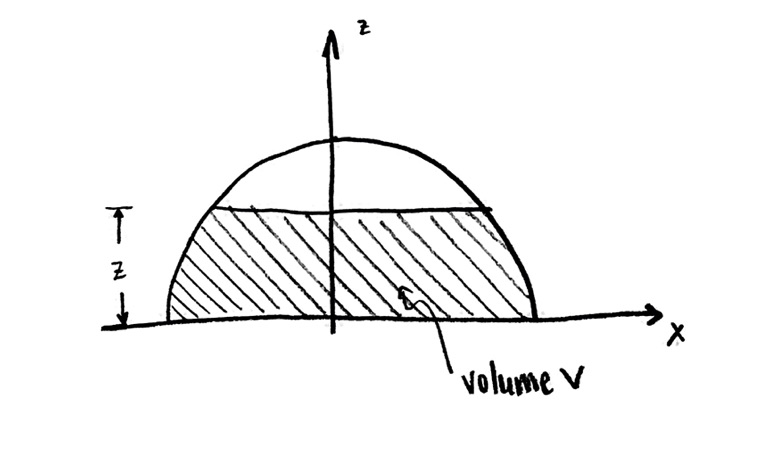
In three dimensions, this looks something like (pardon my poor drawing):
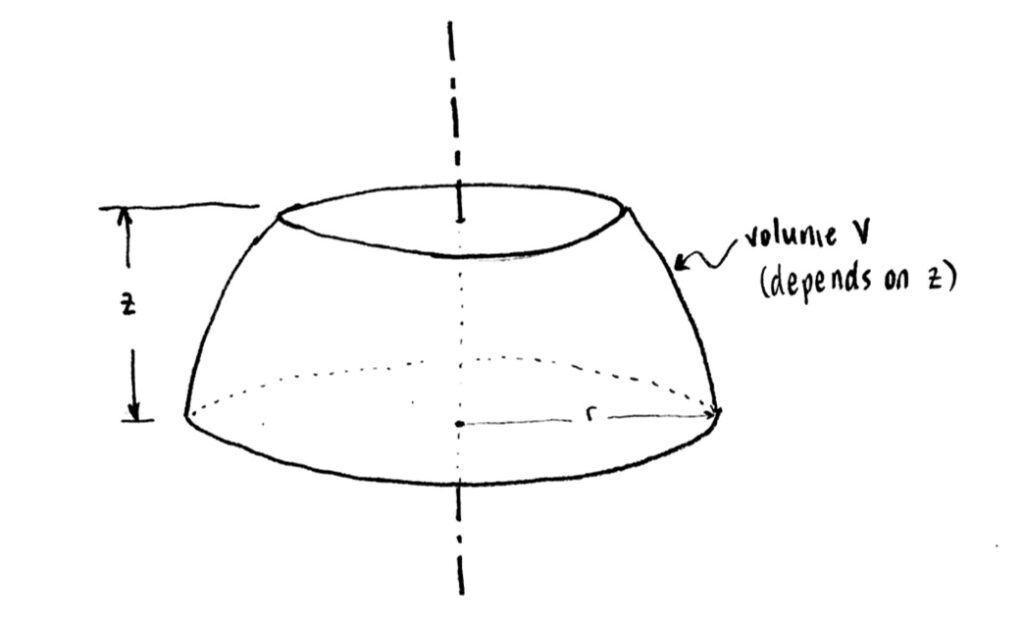
The volume $V$ refers to the volume of water. It now depends on the height to which I’ve filled the tank, the variable $z$.
The problem I was trying to solve originally was to find this volume $V$ when the tank is fully filled, that is, when $z=r$. So why replace it with a harder problem??
The key idea is that now, instead of being a static number I’m trying to find, I’m looking for a dynamic function $V$. The volume $V$ of water in the tank increases as $z$ increases. It is this dynamic nature that lets me use calculus ideas. Here’s how:
Calculus enters!
Now we are trying to find this changing volume $V$, which depends on the height to which we have filled the tank $z$. That is, $V$ has some formula depending on $z$ that we don’t know, and would like to find.
Let’s let $z$ increase a little bit, to $z+\mathrm{d}z$. Then the volume of the water is going to increase, from $V$ to $V+\mathrm{d}V$. Those two changes are going to be related. Let’s see how.
Actually, why don’t you stop and figure out how? See if you can find a formula for $\mathrm{d}V$, which depends on $\mathrm{d}z$, and maybe some other variables. The formula depends on the picture, so you should draw some pictures. Go ahead and try it, I’ll wait!
Problem: Based on the above, find a formula for $\mathrm{d}V$, which depends on $\mathrm{d}z$, and maybe some other variables.
…
…
…
…
… Still working? Don’t look at the answer till you try it!
…
…
…
…
… Really, don’t look at the answer yet!
…
…
…
…
…
…
… Who am I kidding, I can’t stop you. I am just ascii characters.
OK, let’s try to draw the picture. The height $z$ of the water increases to $z+\mathrm{d}z$. In cross-sectional side view, we have something like this:
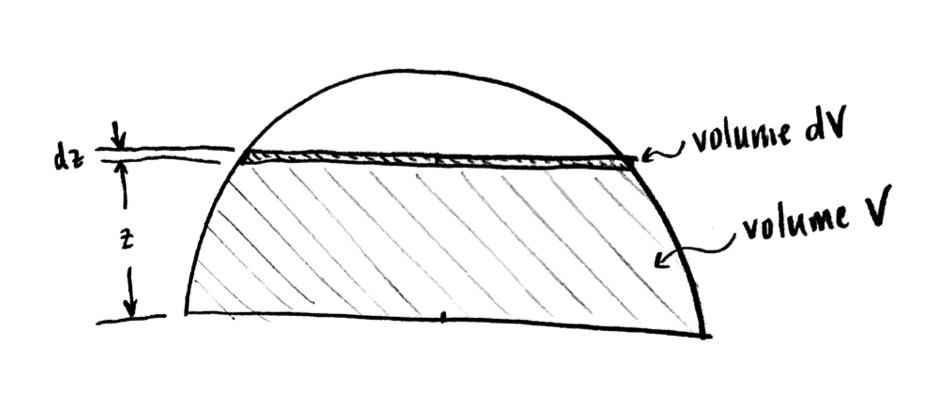
Remember that that little extra slice, of height $\mathrm{d}z$, is actually a three-dimensional volume of water! Its shape in 3-D looks something like:
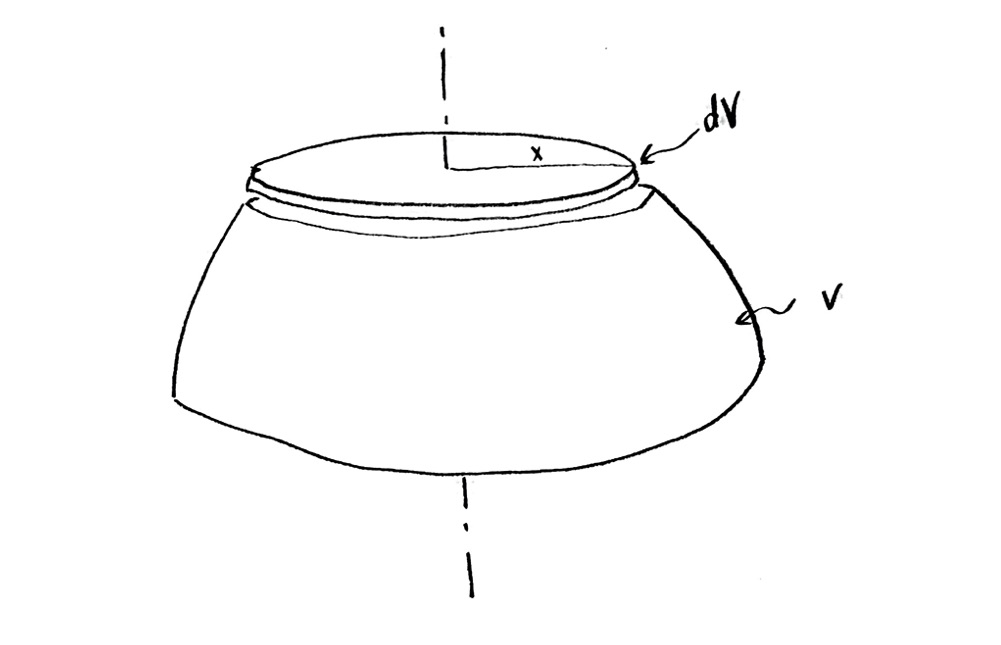
The additional water, of volume $\mathrm{d}V$, has a shape like a pancake or flat disc. I am going to ignore the sloping sides, because I am assuming that the height of the pancake $\mathrm{d}z$ is assumed to be very small.
This means I can find the volume $\mathrm{d}V$! It is the area times the thickness. To find the area, I need the radius, which I don’t really know, so I’ll give it some variable name. Let me call it $x$, since it is in the x-direction in my cross section (but I could have called it anything else). Then my additional volume $\mathrm{d}V$ is $$\mathrm{d}V=\pi x^2\,\mathrm{d}z$$
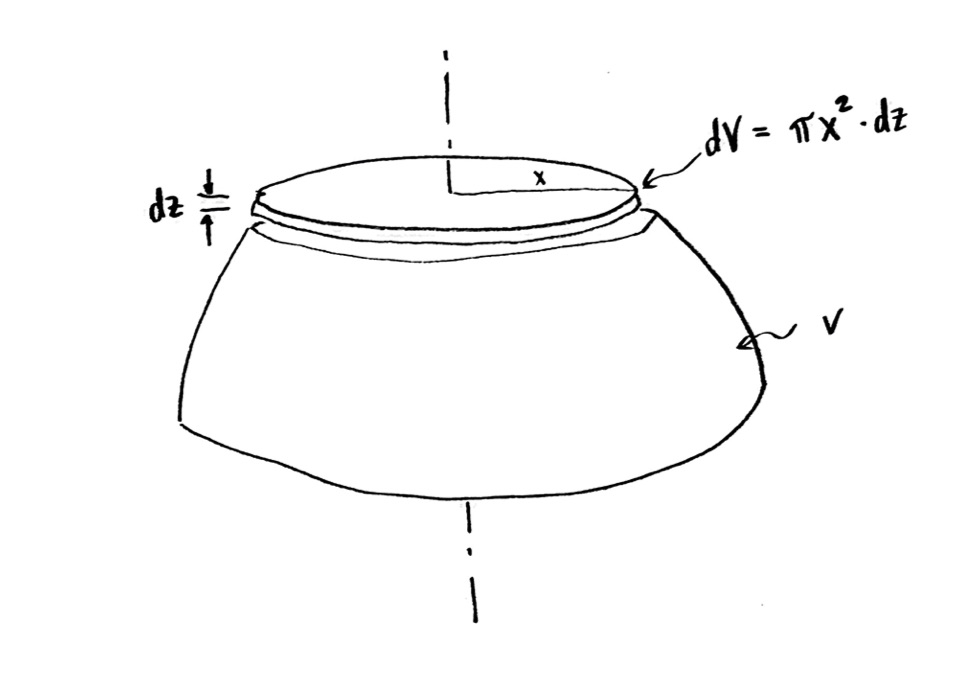
Lovely! But how does this help us?
Problem: How does this help us?
(Try to think it through for a minute before reading on.)
How does this help us?
Here’s the strategy: the volume $V$ of water filled so far is a function. It is a function of the depth $z$ that we have filled so far. So
V = unknown formula of z.
What we have determined is
$\dfrac{\mathrm{d}V}{\mathrm{d}z}=\pi x^2$.
So we know the derivative of the formula we want!
Well, that will be the strategy, but not so fast. The problem is that we don’t really know $x$. To be more precise:
x = unknown formula of z.
So we need to determine $x$ as a function of $z$. If we can do that, then we really will know the derivative $\dfrac{\mathrm{d}V}{\mathrm{d}z}$ as a function of $z$, and then we will be rolling.
Problem: Try to find the dependence of $x$ on $z$. That is, find a formula for $x$ which involves $z$ (and possibly also constants, like $r$ or $\pi$).
Give this a good try before reading the next section!
Dependence of $x$ on $z$
As I said above, I’d like to see how $x$ depends on $z$. Well, let’s draw the cross-section again, with $x$ and $z$ labelled:
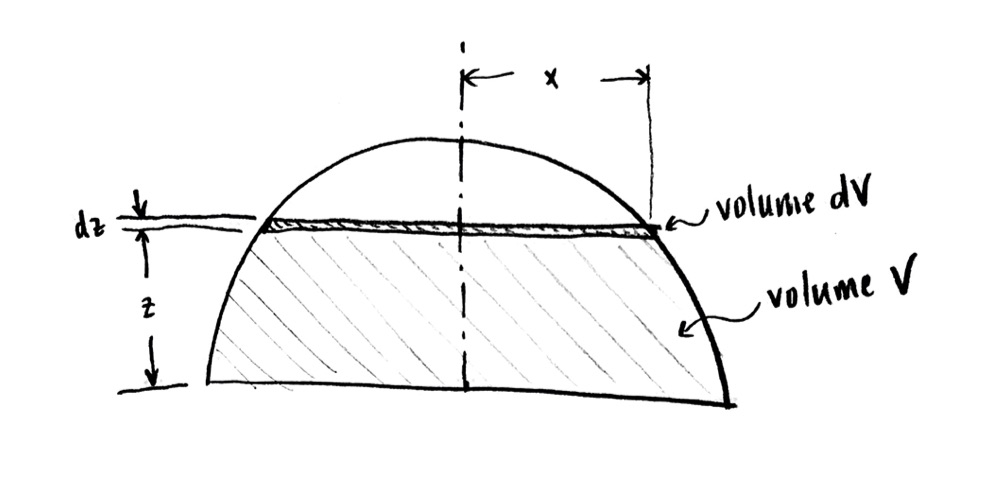
If you haven’t already, try to get the relationship of $x$ to $z$!
…
…
Seriously, it will be more pleasant if you figure it out yourself!
…
…
…
If we were in person I could make you stop, but oh well, all control is an illusion anyways.
Here’s the trick:
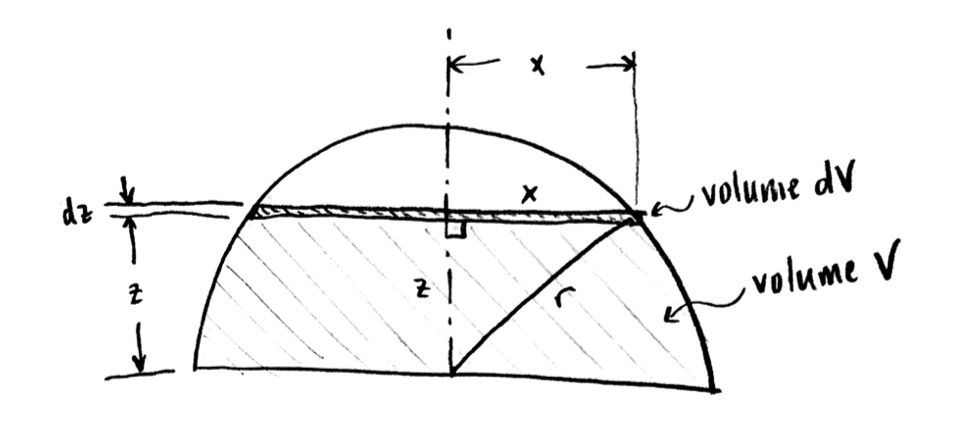
Right?
Because the edge of the disc $\mathrm{d}V$ is on the sphere (or on the circle in cross-section), the distance to the center is the radius $r$. So by good ole’ Pythagoras,
$x^2+z^2=r^2$,
and consequently
$x^2=r^2-z^2$.
I could solve for $x$ by square rootifying, but remember my goal!
Truly knowing the derivative $\frac{\mathrm{d}V}{\mathrm{d}z}$
Now we can really know the derivative $\dfrac{\mathrm{d}V}{\mathrm{d}z}$!! Substituting in what we got before, it is
$\dfrac{\mathrm{d}V}{\mathrm{d}z}=\pi (r^2-z^2)$
or
$\dfrac{\mathrm{d}V}{\mathrm{d}z}=\pi r^2-\pi z^2$.
Magic!
Wait, you don’t believe it is magic?
Let’s recap the story so far:
A quick recap…
We wanted the volume of a sphere of radius $r$. I decided to try to find the volume of a half-sphere, then multiply by 2; fair enough. Then I introduced the crazy idea of trying to find the volume of the partially filled sphere, filled to a height $z$, which apparently made the problem harder:

Terrible! $V$ is a completely unknown function of $z$ (and possibly the constants $r$ and $\pi$. But now look: from the geometry of the situation, we have found the derivative of our unknown function!
$\dfrac{\mathrm{d}V}{\mathrm{d}z}=\pi r^2-\pi z^2$.
Now it’s an algebraic problem! We know the derivative, and we have to find the function it came from. This is going back to the first problem set. Take a moment to look over that work if you don’t recall it.
Finding $V$ from knowing $\frac{\mathrm{d}V}{\mathrm{d}z}$
Problem: Try to find the formula for $V$ as a function of $z$, knowing the formula for its derivative $\dfrac{\mathrm{d}V}{\mathrm{d}z}=\pi r^2-\pi z^2$ that we worked out above.
Really, try to work it out yourself first! It will make more sense than trying to read my solution—unless you get stuck, then read ahead!
Let’s try to solve this problem. First, what formula has a derivative
$\pi r^2$?
Careful!
In this problem, $r$ is NOT a variable. It is a constant. If we had a formula like $\frac{\mathrm{d}V}{\mathrm{d}z}=5$, we would conclude that $V=5z$. So, if $\frac{\mathrm{d}V}{\mathrm{d}z}=\pi r^2$, then $V=\pi r^2 z$. (I’m only doing the first term right now.)
Now, for the other part, $z$ is the variable, and it appears to the second power in the derivative. So the original function must have had a third power: if $\frac{\mathrm{d}V}{\mathrm{d}z}=-\pi z^2$, then $V$=(something)$z^3$. Since the derivative of $z^3$ is $3z^2$, we need to cancel that 3 that appears, so we need $V=-\frac{1}{3}\pi z^3$. (This is only the second term.)
Putting the two pieces together, we find
$V=\pi r^2 z – \frac{1}{3}\pi z^3$,
or, if we feel like simplifying a bit,
$V=\pi z \left(r^2-\frac{1}{3}z^2\right)$.
Magical! We have found a formula for the volume of this weird shape (the partially filled half-sphere)!
Not so fast, the constant!
Wait one minute! We don’t know that is exactly the formula for $V$! We know that
$V=\pi z \left(r^2-\frac{1}{3}z^2\right)$
has a derivative of
$\dfrac{\mathrm{d}V}{\mathrm{d}z}=\pi r^2-\pi z^2$;
but that’s not the only possible answer! Our formula for $V$ could actually be
$V=\pi z \left(r^2-\frac{1}{3}z^2\right)+C$,
where $C$ could be any constant! The $C$ would disappear when we take the derivative, and still give us the same $\dfrac{\mathrm{d}V}{\mathrm{d}z}$.
Here’s how I can figure out the right value of $C$. If the height we fill to is $z=0$, then the volume ought to be $V=0$, right? Substituting those into the equation for $V$, you will find that
$C=0$,
so our first answer of
$V=\pi z \left(r^2-\frac{1}{3}z^2\right)$
was right after all! Phew!
(The constant $C$ won’t always be $0$. For example, if we hadn’t split the sphere in half, we could have done things the same way, but constant wouldn’t come out to zero. We’d get the same answer in the end. In some other problems, you can’t really avoid the $C$!)
So wait, what did we just figure out?
We have found the formula for the volume of a half-sphere, partially filled to a height $z$:

It is
$V=\pi z \left(r^2-\frac{1}{3}z^2\right)$.
Nice!
But our original problem was to find the volume of the sphere!
Well, we get the sphere back if we fill up the whole tank! So if we set $z=r$, we get
Exercise: Substitute in $z=r$ into the formula for $V$ and check that we get…
$V=\frac{2}{3}\pi r^3$
for the volume of the half-sphere; therefore, the whole sphere has volume
$V=\frac{4}{3}\pi r^3$ !!!!
Success at long last!
Wait, does this make sense?
Well, that was a pretty involved argument. How do we know the final answer is right? (Since this is a classic problem, you can look up the answer, but that option isn’t always available!)
First of all, the units are right. If $r$ is in meters, then $V$ will come out in meters cubed, which makes sense.
Second, we could compare to an estimate. If we put the sphere in a box, the box would have volume $8r^3$.
Exercise: Check that.
Our formula gives $V\approx 4.19 r^3$ for the sphere, compared to $V=8r^3$ for the box it is in, so that is at least consistent.
We could get a better estimate by putting the sphere into a cylinder. If we do that, the cylinder would have volume $2\pi r^3$.
Exercise: Check that.
Well, now that looks better: the volume of the cylinder is $\frac{6}{3}\pi r^3$, and the volume of the sphere is $\frac{4}{3}\pi r^3$. So, if our answer is right, the volume of the sphere takes up a fraction $\frac{4}{3}/\frac{6}{3}=\frac{2}{3}$ of the volume of the cylinder containing it, which seems pretty plausible. Doesn’t it?
Try one yourself!
This strategy recurs all through calculus. I’d like to try a similar volume example first. Later we’ll see examples of calculating all kinds of things (and I’ll introduce some more terminology).
Here’s a similar one:
Exercise: Suppose that I have a pyramid with a square base. That is, I start with a square horizontal base, and then I choose a point vertically directly above the center of the square. I connect the top point to the four corners of the square with line segments, then I fill in the four triangles I have created, and finally I fill in the resulting solid.

Let’s say the height is $h$ and the base is $b$.
a) First, before you get started, make a guess about the formula. Try putting the pyramid in a box: what’s the volume of the box? What fraction of the box do you think the pyramid will take up?
b) Then, follow all the steps I did for the sphere, one by one, with the pyramid. At each step, pay attention to what is the same, and to what you need to change.
c) Once you get an answer (it may take a while!), test it out the way I did with the sphere. Does your final answer agree with your guess?
That’s enough for now. I’ll have plenty more variations to ask you about soon!
Update: You can find more problems to develop these ideas in Problem Set #7.
