Category: Advanced Linear Algebra

This will be a combination of written lecture and problem set. I’ll discuss some applications of eigenvalues, and integrate that with suggested problems to try.

Three comments:

• There are more problems here than you can realistically do. There are many of them, and they are open-ended. I am not expecting you to do them all. Pick one problem (or maybe two), and do that problem in as much depth as you have time for.
• In fact, I mentioned at the beginning that you could do a project for this course if you choose. Some of the problems here are open-ended enough that they would make good projects, which you could concentrate mostly on for the rest of the term if you wanted.
• On the other hand, because this lecture focuses on applications, most of the problems are for those of you who are interested in applications and computing. If you are mostly interested in theory, take a look at the questions on Fibonacci numbers and on Spectral Graph Theory; those have some quite interesting theory sides. (The other applications involve a lot of theory too!) But if you are mostly interested in theory, and don’t find any questions to your interest in this problem set, it is OK to skip it entirely; I will have more theory problems on the next problem set that you can do instead!

Google PageRank

We discussed this in class some, so I’ll be brief. Google has two problems in developing search:

• Collecting all the information and storing it, particularly all occurences of keywords, so you can create a list of all websites with a given search word;
• Ranking those search results, so you can get to the most relevant and important websites.

The first problem is largely a (difficult and interesting!) coding and implementation problem. The second problem has a more mathematical component to it.

The great challenge is to determine which website is most “important”, without the algorithm being able to understand the semantic content of any of the websites. (Although people have added evaluations of content to improve search, either by humans or AI, it’s not feasible to expect it for the bulk of search ranking. Most of the job needs to be automated.)

There are two basic ideas:

ignore the content entirely, and only look at the directed graph of outgoing and incoming links

This abstracts away anything about the websites. But with only this very abstracted information, what can we tell? How can we get started?

The second idea addresses this, in a self-referential way. It is that a website is important if other important websites link to it. More quantitatively:

the importance score of a website is proportional to the sum of the importance scores of all the websites that link to it

The first basic idea means that this setup is applicable to many things other than search. It has been used to analyze social networks to determine the “most important” players. In particular, it has been used to analyze terrorist networks, in which the analysts knew the number and direction of electronic messages, but nothing about the people behind the accounts. It has also been used in biology, where interactions between proteins or organisms are known without having details of the nature of the interactions.

The second basic idea is, as I said, essentially self-referential.

The problem below has several parts. Feel free to do just part; get into it in as much depth as you find interesting and have time for. (And feel free to skip it if this isn’t your interest.)

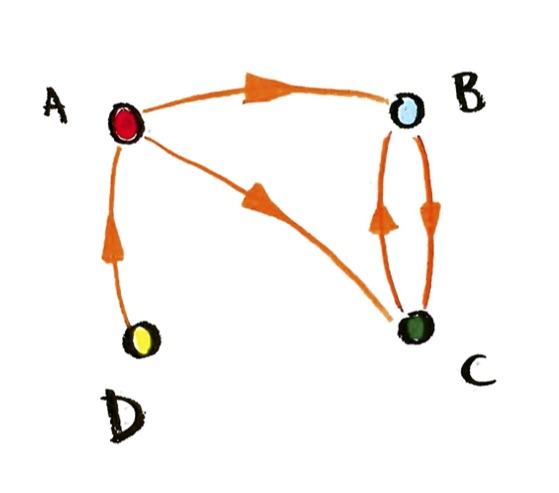
Problem: Google PageRank toy problem and set-up
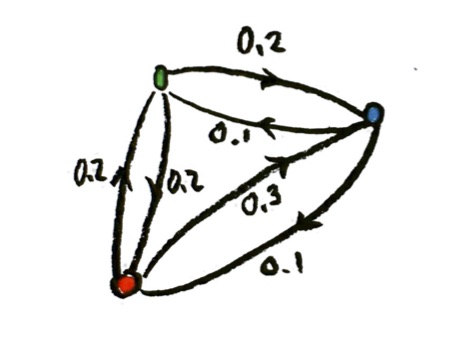
a) Consider the social network that I drew above. We have people A, B, C, and D. An arrow from X to Y represents “X likes Y”. (Or you can think of A, B, C, and D as websites, and an arrow from X to Y represents “X links to Y”.) We are looking for a “popularity” or “importance” score for A, B, C, and D, obeying the rule above: the popularity score of X should be proportional to the sum of popularity scores of all those who like (link to) X. Set up equations expressing this. (Recall that two quantities P and Q are said to be proportional if it is always true that P=kQ, for some constant k.)
b) Write those equations as a matrix equation.
c) Write the matrix equation as an eigenvalue and eigenvector equation.
d) Can you find a non-zero popularity function for this example, which obeys the equation? (You can either try to solve the equations, or look at the graph and think practically.) What is the eigenvalue? Do you think this is typical?
e) Write out what the procedure and the equation would be for any given directed graph.

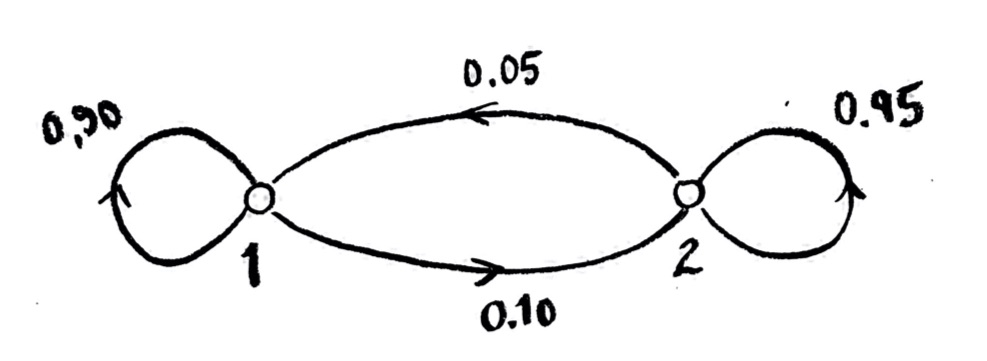
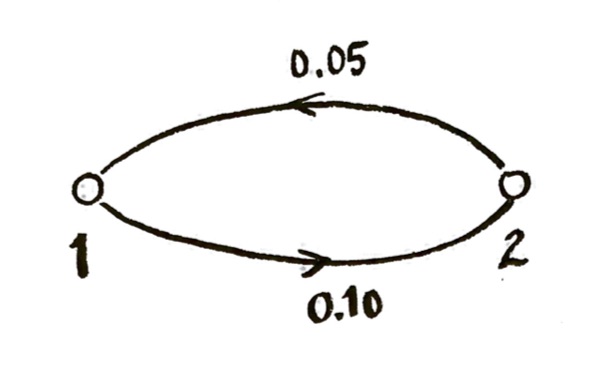
Problem: Google PageRank, Markov processes, and successive approximation
This is an open-ended question, which could be both theory and/or computing. Someone in class had the excellent idea of treating this problem like the Markov process we discussed earlier. We could start with some arbitrarily chosen popularity scores, and then let popularity “flow” through the network, like we did with the Markov system. The idea is that this will make our popularity scores come closer to scores which obey the condition we want. The correct popularity scores would be obtained by iterating over many time steps, to approximate the limit.

This raises two questions which you could look at:
(Theory-ish): Should this work? Can you show that the limit under this process would obey the equations we got in the previous question? Are there some limitations?
(Computing): Try some examples and see if it works!

Problem: Google PageRank existence and uniqueness
This is an open-ended, more theory type question. We have set up equations that we want the popularity/importance scores to satisfy. The questions that always come up in solving a math problem are:
– does there always actually exist a solution (i.e. a non-zero popularity score which obeys our condition)?
– if there exists a solution, is it unique? If not, can we quantify the nature of the set of solutions? (And, for a practical problem, if there are multiple solutions, can we figure out which one to choose?)
This is worth thinking about at least a little bit. It will be tough to solve in general at this point, but even if you can formulate it, that will give you some insight (and relate to other things we will do soon).

Problem: Google PageRank computing examples
This problem is a “computing” problem, and a little more open-ended. It would be interesting to generate a network, set up the matrix eigenvalue equation, and then actually compute the eigenvalues and eigenvectors, and see what the popularity scores look like. This could also give you insight into the above problems, of whether there always exists a solution and if it is unique.

Note that SciPy/SageMath have built-in functions to compute eigenvalues and eigenvectors. I would recommend starting with a small example, like the one above that we did and have some answers for. Then gradually make it bigger: maybe add some extra edges to our A, B, C, D example first. Then try to add more nodes. If you’re feeling ambitious and want larger examples, you could get the computer to randomly make some larger networks. Even if you’re not specifically interested in this sort of computing application, some computer experimentation like this can give you some intuition and insight about how eigenvalues and eigenvectors work for these sorts of matrices!

Problem: Google PageRank further reading
There are a number of good resources about this problem. For this problem, you could start working your way through this paper:
The $25,000,000,000 Eigenvector: The Linear Algebra Behind Google
The paper suggests a more refined version of what I’ve been arguing here, and answers some of the theoretical questions that I mentioned. And there are exercises! If you find this question interesting, working through this paper could be a good final project for the class, that would teach you a lot about the topics we have been working with.

Problem: Computing eigenvalues by powers of a matrix; dominant eigenvalue
In the discussion in class, it came up that for large matrices like in PageRank, the eigenvalues and eigenvectors (particularly the largest, or “dominant” eigenvalue) are often computed by taking powers of the matrix, rather than the method I described in class for small matrices. If you are interested in this topic, you can find an introduction in the first part of the following excerpt (from Kolman and Hill, Elementary Linear Algebra):
Kolman and Hill, Dominant Eigenvalue and Principal Component Analysis
Note that the section starts with the spectral decomposition! For this problem, you could work through the explanations and examples in this handout, and perhaps try a couple of exercises, depending on the depth of your interest in this topic.

Principal Component Analysis

I won’t attempt to write up an explanation here. Rather, I will refer you to some sources. Depending on your level of interest in this topic, I would recommend reading and working through these sources, trying some of the exercises, and perhaps trying an analysis on your own. This could count as a problem set or a project, depending how far you take it. But if you just want the basic idea, you could read through the first sources.

The first things I would recommend reading are the following excerpts from Kolman and Hill, Elementary Linear Algebra. The first one is on the correlation coefficient:
Kolman and Hill, Correlation Coefficient
Understanding this material on the correlation coefficient is not strictly necessary to understand principal components, but it will help you to understand how the basic data analysis is set up, and what the variance is measuring. It’s also interesting in its own right.

The second thing I would recommend reading is also an excerpt from Kolman and Hill, Elementary Linear Algebra:
Kolman and Hill, Dominant Eigenvalue and Principal Component Analysis
If you aren’t specifically interested in dominant eigenvalues in general (see the problem in the previous section), you could skip directly to the section on principal component analysis, and only refer back to the first part of the chapter as needed. I would recommend working through the explanations and examples, and perhaps trying an exercise.

If you want more detail, this tutorial by Lindsay Smith has a nicely paced, detailed explanation of all the elements that go into PCA, with examples:
Lindsay Smith, A Tutorial on Principal Components Analysis.

If you would like to go deeper into PCA, and learn more of the theory, this tutorial by Jonathon Shlens is good:
Jonathon Shlens, A Tutorial on Principal Component Analysis.
If you wanted to work through this tutorial as a project, it would touch on many of the topics that we have covered and also many of those I am planning for the rest of the term.

Markov Processes and Cryptoanalysis

The following article about using Markov processes to decipher messages is quite fun:

Persi Diaconis, The Markov Chain Monte Carlo Revolution

He also talks about other applications of Markov chains as models. The introduction should be readable for everyone, if you’re interested. Section 2 should be mostly possible to understand, based on what we have done, if you take it slowly. This could be an excellent project, to try to work through this section, and maybe to implement a similar model for a problem of this type. Sections 3, 4, and 5 are too advanced for this class, but it might be fun to browse ahead and see what sorts of math is being used (particularly if you took Abstract Algebra or Analysis…)

(Incidentally, Persi Diaconis was known for being both a mathematician and a magician. If you’re interested in magic, gambling, card tricks, etc, it might be interesting to look for some of his other works.)

Fibonacci sequence and discrete dynamical systems

You’ve probably seen the Fibonacci sequence before:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, . . .

Each term in the sequence is the sum of the previous two terms, starting with $f_0=1$ and $f_1=1$:

$f_{n+1}=f_n + f_{n-1}$, for $n=1, 2, 3, \dotsc$.

You may know that there is a relation of the Fibonacci numbers to the “golden ratio” $\phi$:

$\lim_{n\to]infty}\dfrac{f_{n+1}}{f_n}=\phi$,

where $\phi\doteq 1.618033\ldots$. The golden ratio is the proportion of length to height of a “golden rectangle”. A “golden rectangle” is one for which, if you cut off a square, then the remaining rectangle is similar to the original:

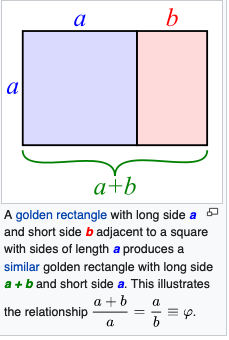
Perhaps more surprisingly, there is an exact formula for the nth Fibonacci number, in terms of the golden ratio:

$f_n=\dfrac{\phi^n-\psi^n}{\phi-\psi}$,

where $\psi=-\dfrac{1}{\phi}$. One of the surprising things about this formula is that there is no apparent reason, looking at it, that it should ever come out to a whole number! (Never mind that it comes out to a whole number for every value of n.)

There are at least two ways of deriving this formula. One is a calculus way, involving infinite series. The other involves linear transformations and eigenvalues. This set of problems is about deriving the closed-form formula above (and generalizing it, if you are interested in going that far).

Problem: Golden Ratio pre-amble
To solve the Fibonacci problem, it will help to figure out some things about the golden ratio first. You don’t have to, you can skip this and press ahead to the next question; but doing this one first will make the computations much cleaner.
a) Find a polynomial equation for the golden ratio $\phi$, based on the defining golden rectangle I mentioned above.
b) Find an exact expression for $\phi$. (Which root of the polynomial is it?)
c) Show that $\phi$ satisfies the equation $\phi^2=\phi + 1$. (If you do it right, this should be immediate, no calculation required!) This equation is quite useful for doing computations with $\phi$. For example, try writing $(2+\phi)^2$ in the form $a+b\phi$, with $a$ and $b$ integers.
d) Write $1/\phi$ in the form $a+b\phi$, for some rational $a$ and $b$.
e) (Theory, optional): The computations above are the main steps in showing that the set of all numbers $a+b\phi$, where $a$ and $b$ are rational, form a field. Complete this proof. (This is very similar to how we construct the field of complex numbers from the field of real numbers.)(This means that the computations below are actually over this field, called $\mathbb{Q}(\phi)$. Fields like this are very important in math.)
f) What is the other root of the defining polynomial for $\phi$? Write this other root in terms of $\phi$. (Hint: work out the factorization of the polynomial in terms of $\phi$.)

Now, here’s the translation of the Fibonacci numbers into a matrix form. I claim that the following equation holds, for any n=1, 2, 3, . . . :

$\begin{bmatrix}f_{n+1}\\f_n\end{bmatrix}=\begin{bmatrix}1 & 1\\1 & 0\end{bmatrix}\begin{bmatrix}f_{n}\\f_{n-1}\end{bmatrix}$.

Exercise:
a) Start with the vector $\begin{bmatrix}1\\1\end{bmatrix}$, corresponding to $n=1$, and multiply by the matrix above (let’s call it $T$) several times, to check numerically that it does in fact generate Fibonacci numbers.
b) (Optional) Prove that the matrix equation given above is valid for all positive integers $n$.

Now, finding Fibonacci numbers means finding large powers of the matrix $T=\begin{bmatrix}1 & 1\\1 & 0\end{bmatrix}$. But we have seen how to do this using eigenvalues and eigenvectors!

Problem: Exact formula for Fibonacci numbers from diagonalization
As we did for the Markov chain example recently, diagonalize the matrix $T$. That is, find the eigenvalues and corresponding eigenvectors of $T$. Write $T$ in the form $T=SDS^{-1}$, where $S$ is the change of basis matrix and $D$ is a diagonal matrix. Conclude that $T^n=SD^nS^{-1}$, and use this to explicitly calculate $T^n$. Finally, apply that to the starting vector $\begin{bmatrix}1\\1\end{bmatrix}$, and simplify, to find the exact formula for Fibonacci numbers.

Suggestions:
– CHECK your work at every stage. For example, if a vector $\vec{e}’_1$ is supposed to be an eigenvector of $T$, multiply it by $T$ and check that $T\vec{e}’_1=\lambda_1\vec{e}’_1$ as it should be. It’s easy to make algebra mistakes in this problem; try to catch them as quickly as possible.
– The computations are much neater if you do them all in terms of $\phi$ and $\psi$, and use the computation tricks I suggested above.
– Your final answer might simplify in a non-obvious way. If you get a final answer that looks different than the one I gave above, try substituting in $n=1,2,3$ into your formula and see if it works! If it does, then you know there is some tricky way to simplify it to the form I gave. It it doesn’t, then you know there is an algebra error somewhere…

Spectral graph theory

This topic is about how the shape of the graph is reflected in the eigenvalues of the graph Laplacian. The graph Laplacian is the operator $\Delta$ that we defined back in the Markov chain example. Since that operator defines diffusion in a graph, there is some intuition about how the eigenvalues connect to heat flow, and how the heat flow connects to the shape of the graph.

People are interested in this problem in both directions: given a graph, what we can say about the eigenvalues; and, computing the eigenvalues, what can we say about the graph. As a general rule, the theory is more in the first question, and the applications are more in the second question. A common type of applied question is, vaguely: we have a big complicated graph, how can we understand the shape and connectivity? And eigenvalues are one tool applied to this sort of question.

If you are interested in learning more, or taking this up as an extended problem/project, there are two ways you could proceed.

1) Experiment! This would be a computing question. Look up, or program yourself, an easy way of storing a graph, converting it to an adjacency matrix, and finding the graph Laplacian $\Delta$. Then, experiment: try different graphs, find their Laplacians, and use Python/SageMath (or whatever you prefer) to compute their eigenvalues. Try graphs that are long and spread out (like a line, or a circle), and compare them to graphs which are more “compact” (like complete graphs).

2) Look at references. There are two sets of slides for talks/tutorials I found that give a pretty understandable introduction. The first is a set of slides by D.J. Kelleher, which I found pretty detailed and readable:
D.J. Kelleher, Spectral Graph Theory.
The second is another set of slides. This one is a little less detailed, but it goes further, and could be a good reference point for learning more:
Daniel A. Spielman, Spectral Graph Theory and its Applications.
You could either read through these references from a more applied perspective—looking for computational problems that you could try out yourself—or from a more theoretical perspective, trying to understand some of the theorems stated.

If you wanted to go further in this topic, there is one best book, written by one of the pioneers and masters of this field:

Spectral Graph Theory, by Fan R.K. Chung, AMS 1997

The library has one copy of this book; if more than one person is interested, let me know, and I’ll try to rustle up another copy! Her book is perhaps a bit advanced for the level of this class, but if you take it slowly it should be comprehensible, and has all kinds of cool stuff in it.

Finite Element Modeling (Physics, Astronomy, Engineering…)

This question is about simulation of physical systems. It is something that is used throughout the physical sciences. Even if you aren’t interested in numerical simulation, it can be very instructive to learn how these models work; in particular, very often the “exact” differential equation models of physics are developed by starting with a discrete finite element model, and then taking the limit as the size of the elements goes to zero.

I will pick one physical problem to look at: wave motion. But the methods work very similarly for other physical problems: quantum wave functions, electric fields, heat flow, stresses, etc etc.

The classic wave motion problem is that of a stretched string with fixed ends (like a guitar string). We imagine that the length, tension, thickness, density, and composition of the string are all fixed at the beginning of the analysis. Depending on the initial motion I give to the string (by plucking or striking), a wide variety of different wave motions are possible:

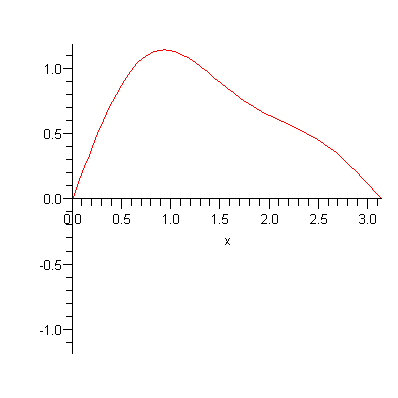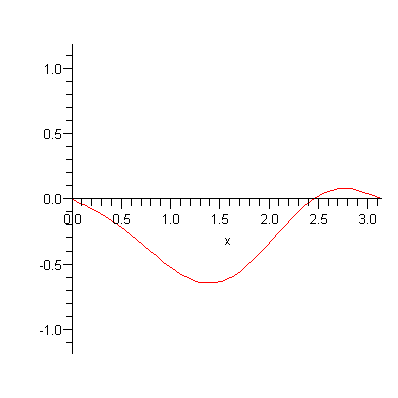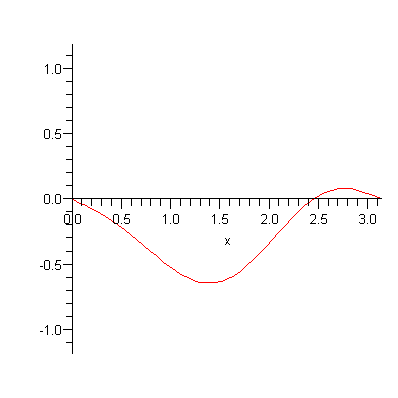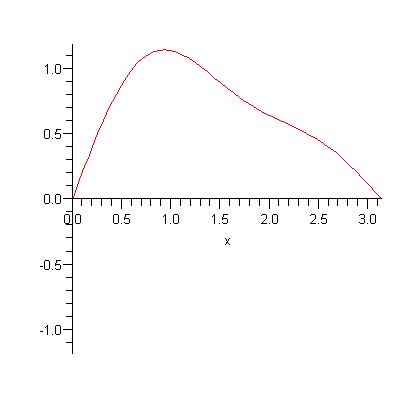
“Finite Element Modeling” means modeling this continuous string with a finite number of discrete pieces. I imagine that, instead of having a string of continuous constant density, I have a number of discrete masses, attached by ideal weightless strings that carry all the force of tension:

The idea is that we can simulate the continuous string by means of figuring out how these discrete masses are going to move. The approximation gets better as we take more, smaller masses, spaced more closely together. (Of course, if the physical system we are interested in really IS a bunch of discrete masses attached by strings, then we are already done: the finite element model will already be a good model!)

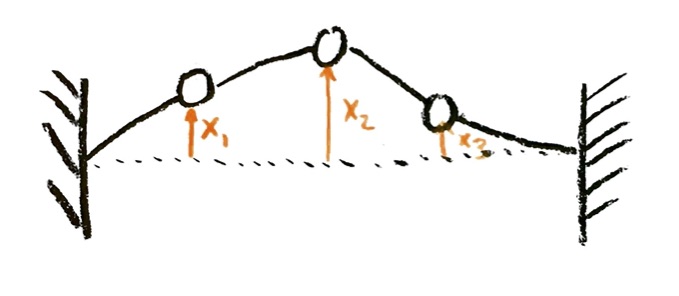
Let’s start with the three masses on a string that I have pictured above. Let’s look at motion in only one direction: assume that the masses can only move vertically in my diagram, not side to side, or in and out of the page. The ends are fixed in position, at the same height. Disregard gravity. The state of the system will then be determined if I know the displacements $x_1$, $x_2$, and $x_3$ of each of the three masses vertically from their rest positions, and also each of the three velocities $v_1$, $v_2$, and $v_3$ in the vertical direction. The value of $x_i$ will be negative if mass $i$ is below the rest position. The value of $v_i$ will be positive if mass $i$ is moving upwards, negative if mass $i$ is moving downwards.

We will collect all the displacements into a displacement vector, and all the velocities into a velocity vector:

$\vec{x}=\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}$, $\vec{v}=\begin{bmatrix}v_1\\v_2\\v_3\end{bmatrix}$.

The vertical force on mass $i$ will have two parts, one from the string connecting to mass $i-1$, and one from the string connecting to mass $i+1$. (If the mass is at the end of the string, “mass $i-1$” or “mass $i+1$” may be replaced by the fixed end. So we might want to introduce the constants $x_0=0$ and $x_{n+1}=0$. In our example, $n=3$ and so we could think of $x_4=0$ for all time.)

To first approximation, the vertical component of the force on mass $i$ from the string to mass $i-1$ will be proportional to the difference in vertical heights of mass $i-1$ from mass $i$. (If you are a physics person, this is a good exercise to verify this claim!) Note that, if $x_{i-1}$ is less than $x_i$, then the force on mass $i$ from that string is downwards.

The constant of proportionality is dependent on lengths of the strings and string tension; let’s just call it a constant $k$.

Problem: Force matrix
a) In the example above, with three masses, write the vertical force $F_1$, $F_2$, $F_3$ on each mass. Each force will depend on the proportionality constant $k$, and also potentially on $x_1$, $x_2$, and $x_3$. (It also depends on $x_0$ and $x_4$, but since these are both the constant 0, you can drop them out in the end.)
b) Write those equations as $\vec{F}=kT\vec{x}$, where $T$ is a matrix.
c) Write out what the matrix $T$ would be if we had a string consisting of $n$ masses (rather than only 3 masses).

Now, the motions are determined by Newton’s law! The vertical acceleration $a_i$ of mass $i$ is given by

$a_i=\dfrac{1}{m_i}F_i$.

Since we have figured out the forces at any given position, we now know the accelerations:

Problem: Acceleration matrix
Show that $\vec{a}=\frac{k}{m}T\vec{x}$, where $T$ is the force matrix you found in the last question.

Now, there are two ways to go. We can leave time as continuous, in which case we get $n$ interlocked differential equations. We know, by definition, that

$\dfrac{\mathrm{d}^2 x_i}{\mathrm{d} t^2}=a_i$.

Since we have formulas for the $a_i$ in terms of the $x_j$, that gives us $n$ interdependent second-order differential equations for the $n$ quantities $x_i$. We can also collect these into one matrix differential equation.

Problem: Second-Order Differential Equations
a) In our example with three masses, write out the three second-order differential equations for $x_1$, $x_2$, and $x_3$.
b) Collect all three differential equations into one matrix differential equation (the left side will be $\dfrac{\mathrm{d}^2 \vec{x}}{\mathrm{d} t^2}$, the right side will be a matrix times $\vec{x}$).
c) How would this look for $n$ masses, rather than three?

It is also often convenient to break these $n$ second-order differential equations into $2n$ linked first-order differential equations. By definition,

$\dfrac{\mathrm{d} x_i}{\mathrm{d} t}=v_i$

and

$\dfrac{\mathrm{d} v_i}{\mathrm{d} t}=a_i$.

Since we have given formulas for the $a_i$, this gives $2n$ first-order differential equations for the $2n$ variables $x_i$ and $v_i$ (instead of $n$ second-order differential equations for the $n$ variables $x_i$).

The other way to approach this would be to also discretize time. We would break time into discrete steps of length $\Delta t$ (this is just a small time step, NOT related to the matrix $\Delta$ from an earlier question!!). In this case, the breaking into first-order differential equations is particularly helpful. We approximate the derivatives by finite differences,

$\dfrac{\mathrm{d} x_i}{\mathrm{d} t}\approx\dfrac{\Delta x_i}{\Delta t}$, $\dfrac{\mathrm{d} v_i}{\mathrm{d} t}\approx\dfrac{\Delta v_i}{\Delta t}$,

which gives us difference equations that approximate the differential equations. In each time step, each $x_i(t_{m+1})$ and $v_i(t_{m+1})$ is calculated by

$x_i(t_{m+1})=x_i(t_m)+\Delta x_i(t_m)$
$v_i(t_{m+1})=v_i(t_m)+\Delta v_i(t_m)$,

where the changes are computed by

$\Delta x_i(t_m)=v_i(t_m)\Delta t$
$\Delta v_i(t_m)=a_i(t_m)\Delta t$.

Here, $v_i(t_m)$ is just the running value of $v_i$ at that time step; but $a_i(t_m)$ stands for the formula for the acceleration of mass $i$, in terms of the various $x_j$, that you computed before.

Problem: Computing with discrete time
(Optional) If you would like to do a computing problem, it is interesting to carry out the computations with discrete time that I have described. Try setting up the discrete time equations, using three masses, and choosing some reasonable value for the constant $k/m$ (you might want to try something like $k/m=0.1$, so it doesn’t jump around too quickly). Then pick some starting value for the $x_i$. See if your simulation gives you something at least half-way realistic for wave motion. (If it’s way off, there is likely an algebra or sign error in there somewhere…)

Now, let’s go back to the differential equation version (continuous time), and see what we can figure out. It turns out that the eigenvectors and eigenvalues of $T$ are crucial here.

Problem: Decoupling equations; role of eigenvalues
a) Suppose that there exists some eigenvector $\vec{e}_1$ of the matrix $T$. Suppose we start the system, at the initial time, with position being a scalar multiple of that eigenvector, $\vec{x}=A_0\vec{e}_1$ for some scalar $A_0$, and with zero velocity. See if you can explain why the system will always have a position $\vec{x}$ that is a scalar multiple $A\vec{e}_1$ (the multiple $A$ changing over time). (It will be easier to give a precise proof after you complete the next parts.)
b) Suppose we have a differential equation

$\dfrac{\mathrm{d}^2 x}{\mathrm{d} t^2}=-Cx$,

for some scalar function of time $x=x(t)$ and some positive constant $C$. Suppose that the initial condition is $x(0)=A_0$, and $v(0)=0$ (zero initial velocity). Show that $x(t)=A_0\cos(\omega t)$ is a solution to the differential equation, with $\omega=\sqrt{C}$. (Just substitute in and check that the equation is satisfied.)
c) Suppose we have a differential equation

$\dfrac{\mathrm{d}^2 A\vec{e}}{\mathrm{d} t^2}=-CA\vec{e}$,

where $A=A(t)$ is a scalar function of time $t$, and $\vec{e}$ is some fixed vector in $\mathbb{R}^n$. Using the previous part, write out the solution of this differential equation. (Write out the vector components to see what this is saying.)
d) Going back to the first part, can you say what the solution of the differential equation is going to be, when the initial positions $\vec{x}_0(0)$ are an eigenvector of $T$? What does this say about the physical motion in this case?

Problem: Eigenvalues and eigenvectors when n=3
a) In our example above, with three masses, find all the eigenvalues and eigenvectors of the matrix $T$.
b) Draw out what the three eigenvectors look like, as positions of the masses on the string. Describe what the motion of each eigenvector (or “mode”) would look like (if we start in one mode, then all positions at later times are scalar multiples of that mode).
c) Describe what the frequencies of each mode are. In particular, say what the frequencies of the second and third mode are, in comparison to the first mode.
d) Diagonalize the matrix $T$. Use this to give a general solution of the differential equation of motion, for any initial condition $\vec{x}(0)$ (and initial velocity $\vec{v}(0)=0$).

This doesn’t work only for stretched strings. For example, we could have a membrane with a fixed edge, like a drum head:

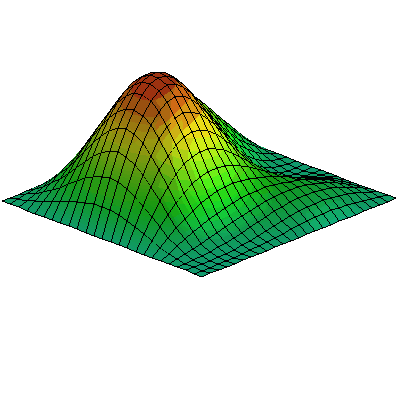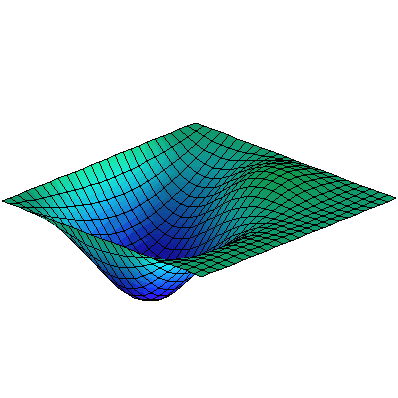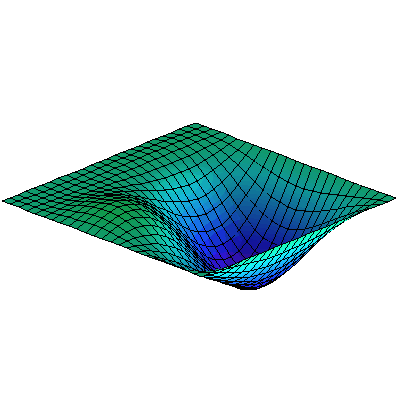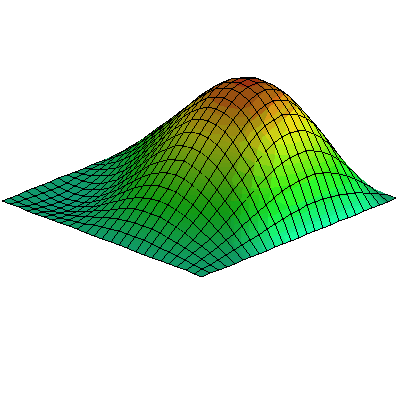
We can set up the finite element model in a similar way.

Problem: Vibrating Membrane
Suppose that we have a square membrane, fixed at the edges, like the picture above. Let’s model this with nine discrete masses, in a $3\times 3$ square grid, connected by a square grid of weightless stretched strings. There are strings attached to a fixed square frame, around the $3\times 3$ grid of discrete masses. The rules will be the same: we only consider vertical displacements $x_i$ and velocities $v_i$, and we assume that the vertical forces are simply proportional to differences in height from neighbors, as before.

Use this setup to write the matrix differential equation as before. Everything should be the same as with the string, except for the $9\times 9$ matrix $T$, which will be different. (Actually, I started kind of large, didn’t I? You might want to try doing a $2\times 2$ grid of masses first, which would give you a $4\times 4$ matrix $T$.)

(I’m not asking you to do any of the later steps here, which would be harder! I’m just asking for the initial setup, which corresponds to finding the matrix $T$.)

There’s plenty more I could ask here, but this is already too much!

Hello again!

I left off the last lecture (Eigenvalues II: Markov processes continued), not so much at a logical stopping point, but just where I got tired and ran out of time! A bit like ordinary class I guess.

In the last lecture, I showed how to

• change basis (coordinates) for a vector
• change basis (coordinates) for a linear transformation
• use a basis made of eigenvectors to simply compute powers of a matrix (applied to the transition matrix for our Markov example)
• use a basis made of eigenvectors to put the matrix of a transformation into simple (diagonal) form
• apply that diagonalization to again simply compute powers of a matrix (this time in matrix form)

At the end of that lecture, I started to show how to use the eigenvectors to decompose the matrix in a different way: as a sum of simple 1-D projection operators (tensor products of vectors and dual vectors). However, I didn’t get very far: I just reminded you about dual vectors, and computed them in our example.

In this lecture, I am going to show how the spectral decomposition works, and apply it to our example.

There is one thing I haven’t told you: how to actually FIND the eigenvectors! I’m going to put that off for a little bit: first I want to show you, in the last lecture and this one, how they are used mathematically (for diagonalization and spectral decomposition), and then in the next lecture to show you some more applications.

OK, let’s get started.

Reminder of our example from last time

To start, I am going to repeat what I said at the end of the previous lecture, for reference.

Recall that our main example was the following two-state Markov chain:

If $x_1$ and $x_2$ are the numbers of agents (or amounts of stuff, or probabilities of one agent) in the two states, then the system state vector $\vec{x}_n=\begin{bmatrix}x_1\\x_2\end{bmatrix}_n$ evolves from time state $t=n$ to $t=n+1$ by the evolution equation

$\vec{x}_{n+1}=T\vec{x}_n = (I+\Delta)\vec{x}_n$.

(I have switched from writing $\begin{bmatrix}x_1\\x_2\end{bmatrix}(t)$, from the last lecture, to $\begin{bmatrix}x_1\\x_2\end{bmatrix}_t$ instead. The former makes sense logically, because the vector is a function of time; however, most people write this the latter way, so it doesn’t get confused with multiplying by t. I’ll stick with the subscript from now on, but it is only a change of notation.)

In our example, the transition operator $T$ is given by the matrix in the $B=\left\lbrace\begin{bmatrix}1\\0\end{bmatrix},\begin{bmatrix}0\\1\end{bmatrix}\right\rbrace$ basis

$[T]_B=\begin{bmatrix}0.90&0.05\\0.10&0.95\end{bmatrix}$,

and the difference operator, or weighted Laplacian, $\Delta$, is given by the matrix

$[\Delta]_B=\begin{bmatrix}-0.10&0.05\\0.10&-0.05\end{bmatrix}$.

Reminder of our analysis so far

We used eigenvectors to better understand the behavior of this system.

The operator $T$ has eigenvectors $\vec{e}’_1=\begin{bmatrix}\frac{1}{3}\\\frac{2}{3}\end{bmatrix}_B$ and $\vec{e}’_2=\begin{bmatrix}1\\-1\end{bmatrix}_B$, with eigenvalues $\lambda_1=1$ and $\lambda_2=0.85$, respectively. The operator $\Delta$ has the same eigenvectors, with eigenvalues $\mu_1=0$ and $\mu_2=-0.15$ respectively.

We showed how to find the first eigenvector, but I did not show you yet how to find the second one. However, once you are given $\vec{e}’_1$ and $\vec{e}’_2$, it is easy to check that they are eigenvectors, and to find the corresponding eigenvalues.

(I could have equally well taken any non-zero scalar multiple of $\vec{e}’_1$ and/or $\vec{e}’_2$, and they would still be eigenvectors, with the same eigenvalues. I picked these particular multiples to make most sense with our example.)

The eigenvectors form a basis, $B’=\left\lbrace\vec{e}’_1,\vec{e}’_2\right\rbrace$. These are also called normal modes for the system.

If I can write my initial conditions in terms of the normal modes, then I can easily compute the operation of $T$ to any power. If my initial condition $\vec{v}_0=\begin{bmatrix}x_1\\x_2\end{bmatrix}_{B\ 0}$ can be written as $\vec{v}_0=x’_1(0)\vec{e}’_1 + x’_2(0)\vec{e}’_2$, then

$T\vec{v}_0=\lambda_1 x’_1(0)\vec{e}’_1+\lambda_2 x’_2(0)\vec{e}’_2$,

so

$T^nvec{v}_0=\lambda_1 ^n x’_1(0)\vec{e}’_1+\lambda_2^n x’_2(0)\vec{e}’_2=1 ^n x’_1(0)\vec{e}’_1+(0.85)^n x’_2(0)\vec{e}’_2$.

We can also so this computation in matrix form. We have the change of coordinate formulas

$[\vec{v}]_{B}=S[\vec{v}]_{B’}$
$[\vec{v}]_{B’}=S^{-1}[\vec{v}]_{B}$,

where $S$ is the change of coordinate matrix, whose columns are the $B’$ basis vectors, expressed in the $B$ basis. In our example,

$S=\begin{bmatrix}\frac{1}{3} & 1 \\\frac{2}{3} & -1\end{bmatrix}$, $S^{-1}=\begin{bmatrix}1&1\\\frac{2}{3} &-\frac{1}{3}\end{bmatrix}$.

We then have the change of coordinate formulas for linear operators,

$[T]_{B’}=S^{-1} [T]_B S$
$[T]_B=S [T]_{B’} S^{-1}$.

In our example,

$[T]_{B’}=\begin{bmatrix}\lambda_1&0\\0&\lambda_2\end{bmatrix}\begin{bmatrix}1&0\\0&0.85\end{bmatrix}$, $[\Delta]_{B’}=\begin{bmatrix}\mu_1&0\\0&\mu_2\end{bmatrix}=\begin{bmatrix}0&0\\0&-0.15\end{bmatrix}$,

and

$[T]_B=S\begin{bmatrix}\lambda_1&0\\0&\lambda_2\end{bmatrix}S^{-1}=\begin{bmatrix}\frac{1}{3} & 1\\\frac{2}{3} & -1\end{bmatrix}\begin{bmatrix}1&0\\0&0.85\end{bmatrix}\begin{bmatrix}1&1\\\frac{2}{3} &-\frac{1}{3}\end{bmatrix}$.

This diagonalization has some nice properties, one of which is that we can easily compute any power of $T$ in the ordinary $B$ basis:

$[T^n]_B=S\begin{bmatrix}\lambda_1^n&0\\0&\lambda_2^n\end{bmatrix}S^{-1}=\begin{bmatrix}\frac{1}{3} & 1\\\frac{2}{3} & -1\end{bmatrix}\begin{bmatrix}1^n&0\\0&(0.85)^n\end{bmatrix}\begin{bmatrix}1&1\\\frac{2}{3} &-\frac{1}{3}\end{bmatrix}$,

and similarly for $\Delta$.

Dual vectors

We have identified that the transition matrix $T$ has a steady-state vector ${\vec{e}’}_1$ given by

${\vec{e}’}_1=\begin{bmatrix}\frac{1}{3}\\\frac{2}{3}\end{bmatrix}$.

That is, the vector stays the same when $T$ is applied to it. (We could have equally well taken any non-zero scalar multiple of ${\vec{e}’}_1$, and that would also be fixed.)

We also mentioned that the total number of agents (or total probability) is fixed: the value

$x’_1=x_1+x_2$

is a constant. This is also a fixed thing, like the fixed/steady-state vector! But it is a different kind of thing: the fixed vector is a vector. This fixed thing $x’_1$ isn’t a vector; it’s a coordinate. More formally, it is a dual vector. And it is fixed, so it is an eigen dual vector. That’s hard to say, so we’ll say dual eigenvector instead.

Given some vector $\vec{v}=\begin{bmatrix}x_1\\x_2\end{bmatrix}_B$, how do I actually find its $x’_1$ and $x’_2$ coordinates? These are found by the dual vectors!

Recall that dual vectors are linear functions $f:V\to k$, whatever our field $k$ is. If they are written as matrices, and $V$ has dimension $n$, then they are $1\times n$ matrices. For this reason, they are also called row vectors.

Recall that the dual basis vectors $\overleftarrow{\phi}’_i$, $i=1,\dotsc,n$, corresponding to the basis $B’=\left\lbrace\vec{v}_i\right\rbrace$, $i=1,\dotsc,n$, are defined by being dual vectors satisfying the condition

$\overleftarrow{\phi}’_i\left({\vec{e}’}_j\right)=\begin{cases}1&i=j\\0&i\neq j\end{cases}$.

It’s not obvious that such dual vectors will always exist for any basis. I’ll ask that as a theory question in the next set of problems.

Assuming there exist these dual vectors, then they are the coordinate functions in the new basis! That is, if we have a vector $\vec{v}$, and it can be written in the new basis as $\vec{v}=x’_1\vec{e’}_1+x’_2\vec{e’}_2+\dotsb x’_n\vec{e’}_n$, then

For $i=1,\dotsc,n$, we have $x’_i=\overleftarrow{\phi}’_i(\vec{v})$.

Understanding exercise: Dual vectors give coordinates
Prove the above statement.

In our two-dimensional example, the $B’$ coordinates of any state vector $\vec{v}$ are given by $x’_1=\overleftarrow{\phi}’_1(\vec{v})$ and $x’_2=\overleftarrow{\phi}’_2(\vec{v})$.

How do I actually find the dual vectors? That is, how do I give their matrices in ordinary $B$ coordinates?

As a practical matter, you can use the defining conditions on the dual basis to set up linear equations for the matrices for the dual vectors, and solve. However, the dual basis matrices are actually already hidden in the change of coordinate matrices $S$ and $S^{-1}$ that we just talked about!

I claim that

the rows of $S$ are the matrices of the $B$ dual vectors, expressed in $B’$ coordinates, i.e. the $i$th row of $S$ is $[\overleftarrow{\phi}_i]_{B’}$,

and consequently that

the rows of $S^{-1}$ are the matrices of the $B’$ dual vectors, expressed in $B$ coordinates, i.e. the $i$th row of $S^{-1}$ is $[\overleftarrow{\phi}’_i]_{B}$.

This last thing is what we wanted. So, if we recall that

$S^{-1}=\begin{bmatrix}1&1\\\frac{2}{3} &-\frac{1}{3}\end{bmatrix}$,

we find that the dual vectors $\overleftarrow{\phi}’_1$ and $\overleftarrow{\phi}’_2$ have bases in the regular $B$ basis given by

$[\overleftarrow{\phi}’_1]_B=\begin{bmatrix}1&1\end{bmatrix}_B$
and
$[\overleftarrow{\phi}’_2]_B=\begin{bmatrix}\frac{2}{3} &-\frac{1}{3}\end{bmatrix}_B$ .

Understanding exercise: Computing coordinates with dual basis vectors
Check that this circle of ideas all closes up with a numerical example. Pick some numerical vector $\vec{v}=\begin{bmatrix}x_1\\x_2\end{bmatrix}$. Use the dual vectors above to find its $x’_1$ and $x’_2$ coordinates. Then check, in ordinary $B$ coordinates, that your chosen vector is in fact that linear combination of the $B’$ basis vectors: that is, check that $\vec{v}=x’_1\vec{e}’_1+x’_2\vec{e}’_2$.

Understanding exercise: Finding dual basis vectors from the change of coordinate matrix
a) See if you can explain why the statement I made is true: that the rows of the change of coordinate matrix $S$ are the matrices of the $B$ dual basis vectors, written in the $B’$ coordinates. To do this, you’ll have to think conceptually about what everything means. (I’m not looking for a formal proof here; I’ll ask that as a theory problem in a little bit. I’m just looking for a reason.)
b) Explain why that means that the rows of $S^{-1}$ are the matrices of the $B’$ dual basis vectors, written in the $B$ coordinates. (Which is usually what we want to find.)

In fact, we can write down change of coordinate formulas for dual vectors. If $f:V\to k$ is any dual vector, and if $S$ is the same change of coordinate matrix that we defined earlier (whose columns are the $B’$ basis vectors written in the $B$ basis), then

$[f]_{B’}=[f]_B S$, and
$[f]_B=[f]_{B’} S^{-1}$.

Understanding exercise: Change of coordinates for dual vectors
a) Try to explain to yourself why these formulas must be correct. (I’ll ask for a more formal proof later, but you could try to give one now if you’re interested.)
b) Use these formulas to solve the previous exercise. (Hint: what are the matrices $[\overleftarrow{\phi}_1]_B$ and $[\overleftarrow{\phi}_2]_B$? What are the matrices $[\overleftarrow{\phi}’_1]_{B’}$ and $[\overleftarrow{\phi}’_1]_{B’}$?

The spectral decomposition

Let’s look again at our example operator $T$. Using the eigenbasis $B’$, we can describe the action of $T$ as follows:

$T\vec{v}=\lambda_1 x’_1\vec{e}’_1+\lambda_2 x’_2\vec{e}’_2$.

That is, given any vector $\vec{v}$, we can calculate $T\vec{v}$ as follows:

• find the $x’_1$ and $x’_2$ coordinates of the vector $\vec{v}$;
• multiply the $x’_1$ coordinate by the corresponding basis vector $\vec{e}’_1$, and multiply that result by the eigenvalue $\lambda_1$;
• do the same for the second coordinate;
• and finally, add the results.

Well, we can write the instruction “find the $x’_1$ coordinate of $\vec{v}$” as a formula now! It is

$x’_1=\overleftarrow{\phi}’_1(\vec{v})$,

and similarly for $x’_2$. Consequently, we can write the recipe above as a formula: for any vector $\vec{v}$, we have

$T\vec{v}=\lambda_1 \overleftarrow{\phi}’_1(\vec{v})\vec{e}’_1+\lambda_2 \overleftarrow{\phi}’_2(\vec{v})\vec{e}’_2$.

I want to write this as an operator formula; that is, I want to leave out the “$\vec{v}$” in the formula. So I could write something like

$T=\lambda_1 \overleftarrow{\phi}’_1(-)\vec{e}’_1+\lambda_2 \overleftarrow{\phi}’_2(-)\vec{e}’_2$,

where the blank “$-$” is supposed to represent where I substitute in the argument $\vec{v}$. This is an odd way to write a function. So I define the notation $\vec{e}’_1\otimes\overleftarrow{\phi}’_1$. This thing is defined to be a linear function, which takes an input in $V$ and an output in $V$. It is defined to operate on an input $\vec{v}$ as follows:

$\vec{e}’_1\otimes\overleftarrow{\phi}’_1(\vec{v}):=\overleftarrow{\phi}’_1(\vec{v})\vec{e}’_1$.

Note that the output is a vector, so it is indeed a linear function from $V$ to $V$. It is called the tensor product, or outer product, of $\vec{e}’_1$ and $\overleftarrow{\phi}’_1$.

Using this notation, I can write

$T=\lambda_1 \vec{e}’_1\otimes\overleftarrow{\phi}’_1+\lambda_2 \vec{e}’_2\otimes\overleftarrow{\phi}’_2$.

This is called the spectral decomposition of the operator $T$. (The set of eigenvalues of the operator are called its spectrum. This is because the spectral lines in chemistry are computed by means of eigenvalues of an operator (a story for next term!).)

What does the spectral decomposition mean?

What kind of a thing is $\vec{e}’_i\otimes\overleftarrow{\phi}’_i$. First I want to describe it conceptually, and then explicitly in coordinates.

Conceptually, any vector $\vec{v}$ can be written as a linear combination of vectors in the $B’$ basis,

$\vec{v}=x’_1\vec{e}’_1+\dotsb+x’_n\vec{e}’_n$.

Let’s look at the meaning of the first coordinate. In the language we introduced earlier, the vector space $V$ is direct sum of the subspaces $V_1=\mathrm{span}\lbrace\vec{e}’_1\rbrace$ and $V’=\mathrm{span}\lbrace\vec{e}’_2,\dotsc\vec{e}’_n\rbrace$. The projection of a vector $\vec{v}$ onto $V_1$, along $V’$, is, by definition, $P_{V_1}^{V’}(\vec{v})=x_1\vec{e}’_1$.

The $x’_1$ is the first coordinate of $\vec{v}$ in the $B’$ basis; the product $x’_1\vec{e}’_1$ is the (vector) projection of $\vec{v}$ onto that first coordinate axis, along all the other coordinate axes.

Therefore, the tensor product $\vec{e}’_1\otimes\overleftarrow{\phi}’_1$ is a projection operator! It is the projection $P_{V_1}^{V’}$, where $V_1$ and $V’$ are defined as above.

The spectral decomposition of $T$ is a decomposition of $T$ as a linear combination of 1-D projection operators.

Let me be more specific in our two-dimensional example. Let’s call

$P_1:=\vec{e}’_1\otimes\overleftarrow{\phi}’_1$ and
$P_2:=\vec{e}’_1\otimes\overleftarrow{\phi}’_2$,

and let’s define $V_1=\mathrm{span}\lbrace\vec{e}’_1\rbrace$ and $V_2=\mathrm{span}\lbrace\vec{e}’_2\rbrace$. Then

$P_1=P_{V_1}^{V_2}$ and
$P_2=P_{V_2}^{V_1}$.

The projections $P_1$ and $P_2$ split $\vec{v}$ into its parts along the $\vec{e}’_1$ and $\vec{e}’_2$ axes.

If I add those parts back again, I get the vector $\vec{v}$ back! So, for any vector $\vec{v}$,

$\vec{v}=P_1(\vec{v})+P_2(\vec{v})$,

which means that

$I=P_1+P_2$.

This is called a decomposition of the identity. It gives the identity operator as a sum of 1-D projection operators. Any choice of basis gives a decomposition of the identity in this way.

We then also have that

$T=\lambda_1 P_1 + \lambda_2 P_2$.

This is again the spectral decomposition of $T$. It writes $T$ as a linear combination of 1-D projection operators. The coefficients of the linear combination are the eigenvalues. Any time we can form a basis out of the eigenvectors of a transformation, we get such a spectral decomposition.

These projection operators obey some very nice algebraic properties, which help make the spectral decomposition useful. First, any projection operator $P=P_{V’}^{V”}$ for a direct sum $V=V’\oplus V”$ (including the $P_1$ and $P_2$ we have defined) satisfies the following identity:

$P^2=P$.

Understanding exercise: Defining equation of projections
a) Try to explain why the equation $P^2=P$ has to be true for any projection.
b) (Tougher; to think about) If a linear transformation $P:V\to V$ satisfies $P^2=P$, do you think it must be a projection? Why or why not?

Second, these particular projections, associated to the basis vector, are “mutually annihilating”:

$P_1P_2=0$, and $P_2P_1=0$.

Understanding exercise: Mutually annihilating projections
a) Try to explain why the equations above must be true.
b) (Tougher; to think about) Can you see what property of a basis (or of a direct sum) is expressed in these equations?

Together, they make algebra quite simple.

Understanding exercise: Computing with projections
a) Using $T=\lambda_1 P_1 + \lambda_2 P_2$, show that $T^2=\lambda_1^2 P_1 + \lambda_2^2 P_2$. (Just do the algebra abstractly, using the symbols, and using the two rules for $P_1$ and $P_2$ I gave above. Don’t try to write matrices or anything.)
b) We should of course have that $I^2=I$. Check that this works with $I=P_1+P_2$.

Writing out the tensor products and spectral decomposition as matrices

I claimed above that the tensor product $P_1:=\vec{e}’_1\otimes\overleftarrow{\phi}’_1$ is a linear function, $P_1:V\to V$. It inputs any vector in $V$, and it outputs a the vector in $V$ which is the part of $\vec{v}$ along the $\vec{e}’_1$ axis.

But if $P_1:V\to V$ is linear, that means $P_1$ has a matrix! How do we calculate it?

One way is to use the meaning of a matrix. If I am trying to find the matrix $[P_1]_B$ of the operator $P_1$ with respect to the standard $B$ basis, then the rule is that the first column of $P_1$ should be $[P_1(\vec{e}_1)]_B$, the effect of P_1 on the first $B$ basis vector, written in the $B$ basis. Similarly for the second column. But these can be figured out based on the definition of $P_1$ and on what we know already, right?

Understanding exercise: Computing matrix of tensor product $P_i$ using definition
a) Follow what I have said above to work out the matrix for $P_1$ in the standard basis.
b) Do the same for $P_2$.

Here’s a slightly easier way. We know that an $m\times n$ matrix over the real numbers represents a linear function from $\mathbb{R}^n$ to $\mathbb{R}^m$, right? So, for example, any dual vector $f:\mathbb{R}^2\to\mathbb{R}$ must be represented by a $1\times 2$ matrix.

Well, if we write vectors in $\mathbb{R}^2$ as $2\times 1$ matrices, then we could see any vector $\vec{v}$ as being a function from $\mathbb{R}$ to $\mathbb{R}^2$, right?

Understanding exercise: Vectors as linear functions
If I interpret a vector in $\mathbb{R}^2$ as being a function from $\mathbb{R}$ to $\mathbb{R}^2$, by matrix multiplication, then what does this function do, geometrically? What does the range of the function look like?

Using this interpretation, I claim that the tensor product is actually composition! That is, claim that, for any vector $\vec{v}$,

$\vec{e}’_1\otimes\overleftarrow{\phi}’_1(\vec{v})$

is the same thing as

$\vec{e}’_1\left(\overleftarrow{\phi}’_1(\vec{v})\right)$,

where we interpret $\vec{e}’_1$ as a function from $\mathbb{R}$ to $\mathbb{R}^2$ as I described above.

Understanding exercise: Tensor product is composition
Do you believe what I just said? Try to think it through. If it’s confusing, read ahead, and then come back to this question.

All this fancy language is to make a pretty simple claim: I claim that the tensor product

$P_1=\vec{e}’_1\otimes\overleftarrow{\phi}’_1$

can be written as a matrix by simply multiplying the matrix of $\vec{e}’_1$ with the matrix of $\overleftarrow{\phi}’_1$:

$[P_1]_B=[\vec{e}’_1]_B[\overleftarrow{\phi}’_1]_B$

and similarly for $P_2$.

Understanding exercise: Computing tensor products $P_i$ by matrix multiplication
a) Check the dimensions of the claimed matrix multiplication above: will $P_1$ come out as a $2\times 2$ matrix, as it should?
b) Make the matrix multiplication, to compute $[P_1]_B$.
c) Do the same for $[P_2]_B$.
d) Check that you get the same thing as you did earlier, using the definition of the matrix.
e) If these are the correct projection matrices, then it should be the case that $P_1+P_2=I$. Is that true for the matrices $P_1$ and $P_2$ that you wrote?
f) The projection matrices were supposed to satisfy $P_1^2=P_1$, $P_2^2=P_2$, and $P_1P_2=P_2P_1=0$. Do they??
f) For our long-running example matrix $T$, it should be true that $T=\lambda_1 P_1 + \lambda_2 P_2$. Check that this is actually true for the matrices $P_1$ and $P_2$ that you wrote!

Once you have solved that last exercise, we have finally written the spectral decomposition for $T$ as explicit matrices!

Before we end, let me ask one last check on your understanding:

Understanding exercise: Projections in basis B’
In all of the above, I’ve been trying to write the projection matrices $P_1$ and $P_2$ in the ordinary basis $B$. What if I tried to find the matrices $[P_1]_{B’}$ and $[P_2]_{B’}$, the matrices in the $B’$ basis, instead? What would those be?

Why?

Why have I been so interested in this spectral decomposition? At the moment, it just seems like a re-writing of the diagonalization of the matrix of an operator.

One reason is that it gives a better conceptual explanation of what “diagonalizing a matrix” actually means. We are writing the transformation as a sum of projection operators.

A second reason is that some of the applications we are headed for next make better sense when you think of them in terms of spectral decompositions, rather than as diagonalizations.

A third reason is that these ideas are going to be important for compression. A large matrix $T$ typically has a few relatively large eigenvalues, and lots of smaller ones. The amount of information in the matrix is $n\times n$ values; the amount of information in each projection operator $P_i$ is $n+n=2n$ values. If $n$ is large, that is a lot smaller. If we keep only the $P_i$ in the spectral decomposition corresponding to the few biggest eigenvalues, we get a good approximation for $T$, but using far less information.

Writing linear transformations as sums of tensor products is going to be a good warmup for tensors, which I’m definitely still hoping we have time for!

Finally, the spectral decomposition is very important in extensions and applications of linear algebra that we sadly won’t have time to get to in this class, like infinite-dimensional spaces and quantum mechanics.

OK, enough trying to sell you on this!

What next?

The next thing I will give you is a problem set, with more examples and problems based on these three lectures (Eigenvalues I, II and III). I will include some Theory problems and some Computation problems, for those of you interested in either of those.

After that, I am planning to give you some material on other applications of eigenvectors, eigenvalues, diagonalization, and spectral decomposition.

Then, I want to introduce inner products. We have forgotten about perpendicularity for a while—I want to bring it back (in more sophisticated form)!

In this lecture, I will return to the Markov chain that I introduced in the previous lecture. I want to provide answers for some of the questions I asked you there, particularly about finding an equilibrium state. But I also want to go further and show how to simplify the evolution, using eigenvectors. In the process, I will connect back to the material we have been doing on dual vectors and projections.

The example Markov chain from last time

Let me remind you of the example from last time. I had a system of agents that could be in two states, 1 or 2. I start with $x_1(0)$ agents in state 1, and $x_2(0)$ agents in state 2. In each time step, some agents would change states, summarized by the following graph:

In each time step, $0.10$ of the agents in state 1 would switch to state 2, and $0.05$ of the agents in state 2 would switch to state 1.

Alternately, this can model only one agent, or system, which changes states with some probabilities. Then $x_1(t)$ and $x_2(t)$ are the probabilities of the single system being in state 1 or 2 respectively.

The goal is to understand, as completely as possible, the behavior of $x_1(t)$ and $x_2(t)$ as functions of time.

The evolution equations we set up last time

In the last lecture, we set up the evolution equation. It is:

$\begin{bmatrix}x_1\\x_2\end{bmatrix}(t+1)=T\begin{bmatrix}x_1\\x_2\end{bmatrix}(t)$,

where the transition matrix $T$ for this system is

$T=\begin{bmatrix}0.90&0.05\\0.10&0.95\end{bmatrix}$.

Alternatively, we can write the evolution equation in terms of differences. The change from time step $t$ to $t+1$,

$\Delta\begin{bmatrix}x_1\\x_2\end{bmatrix}(t):=\begin{bmatrix}x_1\\x_2\end{bmatrix}(t+1)-\begin{bmatrix}x_1\\x_2\end{bmatrix}(t)$,

is given by

$\Delta\begin{bmatrix}x_1\\x_2\end{bmatrix}(t)=\Delta\begin{bmatrix}x_1\\x_2\end{bmatrix}(t)$.

Oops, that equation looks silly, doesn’t it!? It’s because I have two clashing notations here (which are totally standard, so I don’t want to change them). The greek capital Delta, “$\Delta$”, on the left refers to “change in the vector”. But the same symbol $\Delta$ on the right refers to what is called the weighted graph Laplacian matrix,

$\Delta=\begin{bmatrix}-0.10&0.05\\0.10&-0.05\end{bmatrix}$,

which is multiplied by the vector.

Anyway, that means that, for each time step $t$,

$\begin{bmatrix}x_1\\x_2\end{bmatrix}(t+1)=\begin{bmatrix}x_1\\x_2\end{bmatrix}(t)+\Delta\begin{bmatrix}x_1\\x_2\end{bmatrix}(t)$,

which means

$\begin{bmatrix}x_1\\x_2\end{bmatrix}(t+1)=(I+\Delta)\begin{bmatrix}x_1\\x_2\end{bmatrix}(t)$,

where $I=\begin{bmatrix}1&0\\0&1\end{bmatrix}$. There are some advantages to writing it both ways.

Finding the steady state

The first question I asked is, does this system approach an equilibrium state? If I start with $x_1(0)$ agents in state 1, and $x_2(0)$ agents in state 2, will the number of agents $x_1(t)$ and $x_2(t)$ settle down over time, or will they oscillate (or even jump around chaotically?). And if they do settle down, what will the equilibrium values be, and how will they depend on the initial values $x_1(t)$ and $x_2(t)$?

We can say that we are looking for possible vectors $\begin{bmatrix}x_1\\x_2\end{bmatrix}$ with the property that

$T\begin{bmatrix}x_1\\x_2\end{bmatrix}=\begin{bmatrix}x_1\\x_2\end{bmatrix}$;

so the transition from time step $t$ to $t+1$ doesn’t change the values.

This is connected to the eigenvectors I talked about in the previous lecture. Such a vector would be an eigenvector for the matrix $T$, with eigenvalue of 1.

We could set this up as linear equations and solve. But there is a trick which makes it a little easier. If I write $T=I+\Delta$, then a steady state vector would have the property that it doesn’t change under the evolution equation. So we’re looking for possible vectors $\begin{bmatrix}x_1\\x_2\end{bmatrix}$ with the property that

$\Delta\begin{bmatrix}x_1\\x_2\end{bmatrix}=\begin{bmatrix}0\\0\end{bmatrix}$.

That is, the vectors we are looking for are eigenvectors of the matrix $\Delta$ as well, with eigenvalue 0. (Note that my definition of eigenvector requires that the vector be non-zero. The zero vector would satisfy this equation, but wouldn’t be very helpful.)

Another word for this is that the vector $\begin{bmatrix}x_1\\x_2\end{bmatrix}$ is in the kernel of matrix $\Delta$. I’ll have more to say about kernels soon.

Anyway, the system $\Delta\vec{x}=\vec{0}$ is a little easier to solve.

Understanding exercise: computing the steady-state vectors
a) Solve the system $\Delta\vec{x}=\vec{0}$.
b) Check that your solutions are in fact eigenvectors of $\Delta$, with eigenvalue $0$.
c) Check that your solutions are in fact eigenvectors of $T$ as well, with eigenvalue $1$.
d) Can you explain why, practically for this model, that any multiple of a steady state vector is also a steady state vector? (A rough explanation is fine.)
e) Suppose that $A:V\to V$ is any linear transformation, and $\vec{v}\in V$ is an eigenvector of $A$ with eigenvalue $\lambda$. Prove that then, for any non-zero scalar $a$, the vector $a\vec{v}$ is also an eigenvector of $A$, with eigenvalue $\lambda$.
f) Suppose that the initial state is $x_1(0)=100$ and $x_2(0)=0$. Find the steady state that this would approach to.
g) Find the steady state vector, in terms of any given $x_1(0)$ and $x_2(0)$.
h) If the system is interpreted as a single agent, moving between states 1 and 2 with some probabilities, then what are the steady-state probabilities?

You should find that the solution set to $\Delta\vec{x}=\vec{0}$ is

$\left\lbrace\begin{bmatrix}x_1\\x_2\end{bmatrix}:\begin{bmatrix}x_1\\x_2\end{bmatrix}=s\begin{bmatrix}1\\2\end{bmatrix},\,s\in\mathbb{R}\right\rbrace$.

Any non-zero scalar multiple of the vector $\begin{bmatrix}1\\2\end{bmatrix}$ will be an eigenvector of $\Delta$ with eigenvalue $0$, and also an eigenvector of $T=I+\Delta$ with eigenvalue $1$. These are the possible steady states.

If we know the initial numbers of agents $x_1(t)$ and $x_2(t)$, then we can solve for the unknown scalar as well. The trick is that, as I noted last time, this system preserves total number of agents (or preserves probability, if we think of it as a single agent). (There are various names for this condition. In our current context, such a system is called Markov. In physics, it says that this satisfies the continuity equation, or is incompressible.)

Anyhoo, since I know the number of agents is constant over time, the variable

${x’}_1 = x_1+x_2$

is constant in time. Consequently, the steady-state vector will have to satisfy two equations:

$\begin{bmatrix}x_1\\x_2\end{bmatrix}=s\begin{bmatrix}1\\2\end{bmatrix}$, and $x_1+x_2=x_1(0)+x_2(0)$.

Understanding exercise: computing the specific steady-state vector
Solve the above equations, to find the parameter $s$ and therefore the specific steady-state vector.

We obtain for the steady-state vector

$\begin{bmatrix}x_1\\x_2\end{bmatrix}=\dfrac{x_1(0)+x_2(0)}{3}\begin{bmatrix}1\\2\end{bmatrix}$,

or, absorbing the 1/3 into the vector,

$\begin{bmatrix}x_1\\x_2\end{bmatrix}=\left(x_1(0)+x_2(0)\right)\begin{bmatrix}\frac{1}{3}\\\frac{2}{3}\end{bmatrix}$.

If we interpret the model as a single agent, and interpret $x_1(t)$ and $x_2(t)$ as probabilities, then $x_1(0)+x_2(0)=1$, so the steady-state probabilities are

$\begin{bmatrix}x_1\\x_2\end{bmatrix}=\begin{bmatrix}\frac{1}{3}\\\frac{2}{3}\end{bmatrix}$.

In summary: it seems that, no matter where the system starts, that long-term, 1/3 of the agents end up in state 1, and 2/3 of the agents end up in state 2. Or, if it is a single agent, it will keep jumping back and forth, but it will spend 1/3 of the time in state 1, and 2/3 of the time in state 2.

Long-term behavior more precisely

But wait, that’s not really a total answer. We have identified an equilibrium state: if the system is exactly in that state, it will stay there. But will it get there? And will it stay there if it is not exactly in the state? Think of a ball at the very peak of a smooth hill: if it is exactly at the peak, it is in equilibrium and will stay there. But it will almost never end up there from other initial conditions; and if it is slightly away from the peak, it will move away.

If you did the computer experiments, or if you think about the meaning of the model, it should be pretty plausible that the system always moves toward the equilibrium that we identified. Using the machinery of eigenvectors and eigenvalues, we can show that more precisely, and also say exactly how it is moving toward equilibrium. (This analysis will be important in many other areas as well, not just this problem.)

We have already identified one eigenvector of $T$ and $Delta$, the vector

$\begin{bmatrix}\frac{1}{3}\\\frac{2}{3}\end{bmatrix}$,

with eigenvalue 1 for $T$, and eigenvalue 0 for $\Delta$.

I’ll tell you soon how to find another eigenvector for $T$ and $\Delta$. For the moment, I just want to show you how you can use the other eigenvector to compute the evolution easily.

So, let me pull the other eigenvector that I computed earlier out of the oven:

I claim that the vector

$\begin{bmatrix}1\\-1\end{bmatrix}$

is an eigenvector of both $T$ and $\Delta$.

Understanding exercise:
Check this claim, and find the corresponding eigenvalue.

Again, I’ll tell you how I cooked up this vector later. But for the moment, let me show you how I can use it. I’m going to use it two ways:

• I can make a basis out of eigenvectors, and T will be simple in that basis; or
• using dual eigenvectors, I can write T as a sum of projection operators, which puts it in a simple form.

Eigenvalue basis

Here’s the trick of the first method: make a basis (coordinate system) out of the eigenvectors of $T$! This basis will be nicely adapted to expressing the matrix $T$.

So, let $B’=\{{\vec{e}’}_1,{\vec{e}’}_2\}$ be the basis consisting of vectors

${\vec{e}’}_1=\begin{bmatrix}\frac{1}{3}\\\frac{2}{3}\end{bmatrix}$, ${\vec{e}’}_2=\begin{bmatrix}1\\-1\end{bmatrix}$.

Any vector $\vec{v}$ can be uniquely expressed as a linear combination of vectors this basis. I’m going to call the corresponding coefficients the coordinates $x_1’$ and $x_2’$ of the vector $\vec{v}$:

$\vec{v}=x_1\vec{e}_1+x_2\vec{e}_2=x’_1{\vec{e}’}_1+x’_2{\vec{e}’}_2$.

The operators $T$ and $\Delta$ operate very simply on this basis:

$T\left(x_1’\vec{e}_1’+x_2’\vec{e}_2’\right)=x_1’T\left(\vec{e}_1’\right)+x_2’T\left(\vec{e}_2’\right)=\lambda_1x_1’\vec{e}_1’+\lambda_2x_2’\vec{e}_2’$.

All it does is stretch in the $\vec{e}_1’$ direction by the eigenvalue $\lambda_1$, and in the $\vec{e}_2’$ direction by eigenvalue $\lambda_2$. So, if we express $T$ in the basis $B’$,

$T\begin{bmatrix}{x’}_1\\{x’}_2\end{bmatrix}_{B’}=\begin{bmatrix}\lambda_1&0\\0&\lambda_2\end{bmatrix}_{B’}\begin{bmatrix}{x’}_1\\{x’}_2\end{bmatrix}$.

We know that $\lambda_1=1$ and $\lambda_2=0.85$. So, in the basis of eigenvectors, $T$ is represented very simply as a diagonal matrix,

$[T]_{B’}=\begin{bmatrix}1&0\\0&0.85\end{bmatrix}_{B’}$.

In this form, $T$ is quite simple and easy to work with. For example, if you wanted to find the state after 13 time steps, you’d just have to find

$T^{13}\begin{bmatrix}{x’}_1(0)\\{x’}_2(0)\end{bmatrix}_{B’}=\begin{bmatrix}1&0\\0&0.85\end{bmatrix}^{13}_{B’}\begin{bmatrix}{x’}_1(0)\\{x’}_2(0)\end{bmatrix}_{B’}=\begin{bmatrix}1^{13}&0\\0&(0.85)^{13}\end{bmatrix}\begin{bmatrix}x’_1(0)\\x’_2(0)\end{bmatrix}_{B’}$.

No need to do thirteen matrix multiplications!

But, I’m not given the initial data in the $x’_1$, $x’_2$ coordinates, and I don’t want the answer in those weird coordinates either. So I need to change coordinates.

Change of coordinates for a vector: concrete linear equation version

Let’s see how to do this in a concrete way. We’ll make it more systematic in the next section.

Let’s suppose we have initial values $x_1(0)=40$ and $x_2(0)=20$.

Understanding exercise: Change of basis by linear equations
With the initial value vector $\vec{v}(0)=\begin{bmatrix}x_1(0)\\x_2(0)\end{bmatrix}=\begin{bmatrix}40\\20\end{bmatrix}$, find the initial values of the primed coordinates, $x’_1(0)$ and $x’_2(0)$.

Here’s the solution to the exercise above. By the definitions above,

$\begin{bmatrix}x_1(0)\\x_2(0)\end{bmatrix}=\begin{bmatrix}40\\20\end{bmatrix}=x’_1(0){\vec{e}’}_1+x’_2(0){\vec{e}’}_2=x’_1(0)\left(\begin{bmatrix}\frac{1}{3}\\\frac{2}{3}\end{bmatrix}\right)+x’_2(0)\left(\begin{bmatrix}1\\-1\end{bmatrix}\right)$,

so we get the linear equations

$\frac{1}{3}x’_1(0) + x’_2(0)=40$
$\frac{2}{3}x’_1(0) – x’_2(0)=20$.

These have the unique solution $x’_1(0)=60$, $x’_2(0)=20$.

Using eigenbasis to compute transformation

Understanding exercise: Computing powers of T in the eigenbasis
Suppose again that we have starting conditions $x_1(0)=40$ and $x_2(0)=20$.
a) Use the previous exercise to find a simple expression for $x_1(n)$ and $x_2(n)$ for any positive integer $n$.
b) Optional computing exercise: use the expression to make a table of $x_1(n)$ and $x_2(n)$ for $n=1,2,\dotsc,20$.
c) Use the expression to find $x_1(20)$ and $x_2(20)$.
d) Use the expression to find the limit of $x_1(n)$ and $x_2(n)$ as $n$ gets large.

Here’s the solution to the previous exercise. We have

$\begin{bmatrix}x_1\\x_2\end{bmatrix}(1)=T\begin{bmatrix}x_1\\x_2\end{bmatrix}(0)=T\begin{bmatrix}40\\20\end{bmatrix}=T\left((60)\begin{bmatrix}\frac{1}{3}\\\frac{2}{3}\end{bmatrix}+20\begin{bmatrix}1\\-1\end{bmatrix}\right)$
$=(60)T\begin{bmatrix}\frac{1}{3}\\\frac{2}{3}\end{bmatrix}+(20)T\begin{bmatrix}1\\-1\end{bmatrix}=(60)\begin{bmatrix}\frac{1}{3}\\\frac{2}{3}\end{bmatrix}+(20)(0.85)\begin{bmatrix}1\\-1\end{bmatrix}$.

So in the same way, we get

$\begin{bmatrix}x_1\\x_2\end{bmatrix}(2)=T^2\begin{bmatrix}x_1\\x_2\end{bmatrix}(0)=(60)\begin{bmatrix}\frac{1}{3}\\\frac{2}{3}\end{bmatrix}+(20)(0.85)^2\begin{bmatrix}1\\-1\end{bmatrix}$

and so

$\begin{bmatrix}x_1\\x_2\end{bmatrix}(n)=T^n\begin{bmatrix}x_1\\x_2\end{bmatrix}(0)=(60)\begin{bmatrix}\frac{1}{3}\\\frac{2}{3}\end{bmatrix}+(20)(0.85)^n\begin{bmatrix}1\\-1\end{bmatrix}$.

Putting in numbers, we have

$\begin{bmatrix}x_1\\x_2\end{bmatrix}(20)\doteq(60)\begin{bmatrix}\frac{1}{3}\\\frac{2}{3}\end{bmatrix}+(0.775)\begin{bmatrix}1\\-1\end{bmatrix}=\begin{bmatrix}20.775\\39.225\end{bmatrix}$.

In the limit as $n\to\infty$, we have $(0.85)^n\to 0$, and hence the limiting state is $\begin{bmatrix}20\\40\end{bmatrix}$, as we had predicted in the previous section.

Change of coordinates for a vector: systematic matrix version

Let’s do this a little more systematically.

In this section, I’ll work through how to change coordinates for a vector, from the old standard basis to the new basis of eigenvectors. This isn’t specific to this example; it works for any change of basis in a finite-dimensional vector space.

Let

$S=\begin{bmatrix}\frac{1}{3} & 1 \\ \frac{2}{3} & -1\end{bmatrix}$.

I have made the columns of this matrix equal to the new basis vectors, the eigenvectors ${\vec{e}’}_1$ and ${\vec{e}’}_2$. This matrix $S$ has the effect of converting from $x’_1$, $x’_2$ coordinates to the $x_1$, $x_2$ coordinates, because

$S[\vec{v}]_{B’}=S\begin{bmatrix}x’_1\\x’_2\end{bmatrix}=x’_1\begin{bmatrix}\frac{1}{3}\\\frac{2}{3}\end{bmatrix}_{B} + x’_2\begin{bmatrix}1\\-1\end{bmatrix}_B=[x’_1{\vec{e}’}_1+x’_2{\vec{e}’}_2]_B=[\vec{v}]_B$.

Understanding exercise: Change of basis matrix
The logic of that previous equation is important. Let’s check it by trying some examples.
a) Suppose that we start with the vector $\vec{v}={\vec{e}’}_1=(1){\vec{e}’}_1+(0){\vec{e}’}_2$, so that $x’_1=1$, $x’_2=0$, and $[\vec{v}]_{B’}=\begin{bmatrix}1\\0\end{bmatrix}_{B’}$. Check that multiplying this vector $[\vec{v}]_{B’}$ times $S$ gives the vector $[\vec{v}]_{B}$.
b) Do the same thing with the vector $\vec{v}={\vec{e}’}_2$.
c) Think through the logic again of the equation above. (I don’t have anything particular for you to write for this part. This is one of those things in math where you need to do the incantation to yourself about a hundred times before it sticks. . . )

This means that the matrix $S^{-1}$, if it exists, converts from $x_1$, $x_2$ coordinates to $x’_1$, $x’_2$ coordinates. Explicitly:

$S[\vec{v}]_{B’}=[\vec{v}]_{B}$
$S^{-1}S[\vec{v}]_{B’}=S^{-1}[\vec{v}]_{B}$
$I[\vec{v}]_{B’}=S^{-1}[\vec{v}]_{B}$
$[\vec{v}]_{B’}=S^{-1}[\vec{v}]_{B}$

So, to summarize,

$[\vec{v}]_{B}=S[\vec{v}]_{B’}$
$[\vec{v}]_{B’}=S^{-1}[\vec{v}]_{B}$

These are the change of basis equations, which apply for changing coordinates of vectors between any two bases $B$ and $B’$. The matrix $S$ is always defined by having columns equal to the $B’$ basis vectors, written in the $B$ coordinates (i.e., the columns are the coefficients of the $B’$ basis vectors, when they are written as linear combinations of the $B$ basis vectors).

We’ll talk about matrix inverses more generally soon, but for the moment you might want to recall that the inverse of a $2\times 2$ matrix is given by

$\begin{bmatrix}a&b\\c&d\end{bmatrix}^{-1}=\dfrac{1}{ad-bc}\begin{bmatrix}d&-b\\-c&a\end{bmatrix}$.

Understanding exercise: Change of basis example
Use this procedure to redo a previous exercise: show how to write the vector $\begin{bmatrix}40\\20\end{bmatrix}_{B}$ in the $B’$ coordinate system. Check that you get the same answer as before.

Next, I want to use this change of coordinates of vectors, to change coordinates for the transformation $T$.

Change of basis for a linear transformation

Now I want to change basis for the transformation $T$. This is the same thing we did earlier, but I want to do it in matrix form now, rather than as linear equations. This method will apply for any linear transformation $A:V\to V$, from a finite-dimensional vector space to itself. (It also applies to $A:V\to W$ between two different vector spaces, with minor modifications.)

First of all, we know that, in the standard basis $B$, the matrix of $T$ is

$[T]_B=\begin{bmatrix}0.90 & 0.05 \\ 0.10 & 0.95\end{bmatrix}_B$.

We can find $[T]_{B’}$ one of two ways. First, we can change coordinates by means of the matrix $S$. This works conceptually as follows:

• $[T]_{B’}$ expects an input in the $B’$ basis, while $[T]_B$ expects an input in the $B$ basis. $[T]_{B’}$ will output its answer in the $B’$ basis, while $[T]_B$ will output its answer in the standard $B$ basis.
• So, to create $[T]_{B’}$, we need to first take an input in $B’$ coordinates, and then convert it to $B$ coordinates, using $S$.
• Then we have the vector in $B$ coordinates, so $[T]_B$ happily eats it, and spits out its answer, also in $B$ coordinates.
• Since we are looking for the answer in $B’$ coordinates, we must convert the output from $B$ coordinates to $B’$ coordinates, using $S^{-1}$.

Summarizing the above conceptual steps, we arrive at the answer

$[T]_{B’}=S^{-1} [T]_B S$.

This arrangement happens so frequently, it has a name: it is called the conjugate of $[T]_B$ by $S$.

Understanding exercise: change of coordinates of transformation conceptually
Think through that reasoning above a few times. There isn’t anything to write here exactly, but you may want to make up your own shorthand to keep it straight. (Personally I draw little arrows moving right to left, showing how the vector moves through the factors in the equation.) In particular, the tricky thing is to get the $S$ and $S^{-1}$ on the correct sides; be sure that your understanding of the reasoning creates the formula I wrote down, and not the opposite order.

Let’s derive this more explicitly, as equations. (Which is more rigorous, but I find personally harder to keep straight.)

$[T]_{B’}[\vec{v}]_{B’}$
$=[T\vec{v}]_{B’}$
$=S^{-1}[T\vec{v}]_B$
$=S^{-1}[T]_B [\vec{v}]_B$
$=S^{-1}[T]_B S[\vec{v}]_{B’}$

Since we have shown that

$[T]_{B’}[\vec{v}]_{B’}=\left(S^{-1}[T]_B S\right)[\vec{v}]_{B’}$

for every vector $\vec{v}$, it must follow that

$[T]_{B’}=S^{-1}[T]_B S$,

as we got before conceptually.

Understanding exercise: change of coordinates of a transformation formally
Once you read through the argument above, it is instructive to reproduce it on your own. There are a couple of subtle steps that make more sense when you think through them yourself.

Understanding exercise: computing the diagonalizing matrix of T in our example
For the transformation $T$ in our example, we have written down the matrix $[T]_B$, and the matrix $S$. Use this, and the formula above, to compute the matrix $[T]_{B’}$.

The answer you should get is

$[T]_{B’}=S^{-1}\begin{bmatrix}0.90&0.05\\0.10&0.95\end{bmatrix}_B S$
$=\begin{bmatrix}1&0\\0&0.85_{B’}\end{bmatrix}$

We say that this basis diagonalizes the matrix of $T$, and that the matrix $[T]_{B’}$ is diagonal.

We could have also gotten $[T]_{B’}$ directly, by the meaning of the matrix (which I discussed a bit in class and on Problem Set 4, but haven’t written up yet). The first column of $[T]_{B’}$ is the vector $T{\vec{e}’}_1$, expressed in the $B’$ basis. But we know $T{\vec{e}’}_1={\vec{e}’}_1$, which in the $B’$ basis is simply ${\vec{e}’}_1=(1){\vec{e}’}_1+(0){\vec{e}’}_2=\begin{bmatrix}1\\0\end{bmatrix}_{B’}$. We can get the second column of $[T]_{B’}$ similarly.

Understanding exercise: Finding $[T]_{B’}$ directly
Complete that argument, to find the matrix $[T]_{B’}$, and verify it is the same answer as before.

We often want to go the other way, to change from the $B’$ basis to the $B$ basis.

Understanding exercise: Changing transformation from $B’$ basis to $B$ basis
We have already worked out $[T]_{B’}=S^{-1} [T]_B S$. Use this equation to find the matrix $[T]_B$ in terms of the matrix $[T]_{B’}$ (and $S$ and $S^{-1}$).

The answer you get should be

$[T]_B=S [T]_{B’} S^{-1}$.

You see why I was worried about getting the formula in the right order!

Confusingly, this formula is often also called the “conjugation of $[T]_{B’}$ by $S$”. As far as I can tell, authors seem about equally split on whether they write the conjugation of $A$ by $S$ as $S^{-1}AS$ or as $SAS^{-1}$.

One thing that makes this representation nice, is that for any positive integer $n$,

$[T^n]_B=S \left([T]_{B’}\right)^n S^{-1}$.

Understanding exercise: Powers of conjugated transformation
Prove the above formula! (Remember that matrix multiplication is not commutative!)

Understanding exercise: Powers of T in our example
Let $n$ be any positive integer, and let $T$ be the transformation from our example above, with $[T]_B=\begin{bmatrix}0.90&0.05\\0.10&0.95\end{bmatrix}$.
a) Use the above formula to find the matrix for $T^n$ in the standard basis, as a product of matrices.
b) Explicitly multiply out the matrices, to find the individual matrix elements of $T^n$ in the standard basis.
c) Find $T^{20}$.
d) Use the explicit form from (b) to find $\lim_{n\to\infty}T^n$.
e) Use the matrix form from (a) to find $\lim_{n\to\infty}T^n$, and check that you get the same thing.

A brief pause; what next?

Whew, this is getting long!

Take a moment to look over what you have accomplished so far. The key point is to change to a basis made of eigenvectors, in which the matrix representation of the transformation is simple.

It’s getting long, but I don’t want to leave the topic until I show you another way of writing and thinking about how to break up the transformation $T$ in terms of eigenvectors. The result is going to be that $T$ can be written as a linear combination of projections onto lines. This is called the spectral decomposition of $T$. This story requires us to look at dual eigenvectors.

Eigenvectors and dual eigenvectors

We have identified that the transition matrix $T$ has a steady-state vector ${\vec{e}’}_1$ given by

${\vec{e}’}_1=\begin{bmatrix}\frac{1}{3}\\\frac{2}{3}\end{bmatrix}$.

That is, the vector stays the same when $T$ is applied to it. (We could have equally well taken any non-zero scalar multiple of ${\vec{e}’}_1$, and that would also be fixed.)

We also mentioned that the total number of agents (or total probability) is fixed: the value

$x’_1=x_1+x_2$

is a constant. This is also a fixed thing, like the fixed/steady-state vector! But it is a different kind of thing: the fixed vector is a vector. This fixed thing $x’_1$ isn’t a vector; it’s a coordinate. More formally, it is a dual vector.

As before, let’s define the basis $B’=\{{\vec{e}’}_1,{\vec{e}’}_2\}$, where

${\vec{e}’}_1=\begin{bmatrix}\frac{1}{3}\\\frac{2}{3}\end{bmatrix}$, ${\vec{e}’}_2=\begin{bmatrix}1\\-1\end{bmatrix}$

are the eigenvectors of $T$. Now, I want to find the dual vectors $\overleftarrow{\phi}’_1$ and $\overleftarrow{\phi}’_2$ corresponding to this basis. Recall that the dual basis vectors are defined by being linear functions (dual vectors) $\overleftarrow{\phi}’_i:\mathbb{R}^2\to\mathbb{R}$, and by the condition

$\overleftarrow{\phi}’_i\left({\vec{e}’}_j\right)=\begin{cases}1&i=j\\0&i\neq j\end{cases}$.

You can use these conditions to set up linear equations for the matrices for the dual vectors, and solve. However, in one of the lectures, I described how to find the dual vectors by means of the change of coordinate matrix $S$ that we just talked about. Please take a look at that lecture if you don’t recall, to solve the following exercise:

Understanding exercise: Computing dual basis vectors
Find the dual vectors $\overleftarrow{\phi}’_1$ and $\overleftarrow{\phi}’_2$, expressed in the standard basis. These will be $1\times 2$ matrices, since they are linear functions from $\mathbb{R}^2$ to $\mathbb{R}$.

To be continued shortly!

Hi everyone!

OK, I had planned to go in strict logical order from now on, but I just couldn’t do it. I was too worried about 1) running out of time for important things, and 2) taking away emphasis from the central ideas.

So what I’m going to do is start with a key example. Then I’ll talk about theory backing that up, and then a new example, and so on. I am planning to write the foundational lectures still, as we go. But I think this way will make more sense (though I know it doesn’t sound like it from what I just said!).

OK, let’s get started.

Eigenvalues, eigenvectors, and spectral decomposition

First, just a little bit of context and theory. I am not going to use this right away in the example, but this is where I’m heading.

Suppose we have linear transformation $A$ that maps a vector space back to itself, $A:V\to V$. It is interesting to know, in many applications, if $A$ has a fixed point: some vector $\vec{v}\in V$ such that

$A\vec{v}=\vec{v}$.

In fact, a more general thing is often of interest: whether $A$ has an invariant line. A line through origin $L$ would be called invariant if:

for any vector $\vec{v}\in L$, we also have $A\vec{v}\in L$.

A line through the origin is a 1-dimensional subspace, so such a fixed or invariant line is usually called an invariant 1-dimensional subspace.

You should take a moment to convince yourself that $A$ has an invariant line $L$ exactly when there exists a non-zero vector $\vec{v}_0$ with the property that

$A\vec{v}_0 = \lambda \vec{v}_0$, for some scalar $\lambda$.

Understanding Exercise: Eigenvectors and Invariant Lines
Give a rough explanation (to yourself is fine, you don’t have to write it out necesssarily) of the statement above: that $A$ has an invariant line exactly when there is a non-zero vector $\vec{v}_0$ with the stated property. It doesn’t have to be a precise proof (see below).

Such a vector $\vec{v}_0$ is called an eigenvector, and the corresponding scalar $\lambda$ is called an eigenvalue. “Eigen” is German for “proper”, in the sense of “belonging to” (like “property”). In some older texts, eigenvectors are called proper vectors, or characteristic vectors. They are vectors which “belong to” or are “characteristic of” the transformation $A$.

Theory Problem: Eigenvectors and Invariant 1-D Subspaces
Suppose that $A:V\to V$ is a linear transformation as discussed above. Prove the following: if there exists an eigenvector $\vec{v}_0$ for $A$, then the line $L=\mathrm{span}\{\vec{v}_0\}$ is an invariant line (1-D subspace) for $A$. On the other hand, if $L$ is an invariant line for $A$, then any non-zero vector in that line is an eigenvector (and all the vectors in that line share the same eigenvalue).

This simple looking concept ends up being deeply useful in many contexts. Let me get into the examples first, and then I’ll come back to how the eigenvectors play a role in the examples. (In a later lecture, I’ll talk about how eigenvectors and eigenvalues are deeply theoretically important as well.)

A Markov chain: setting up the model

OK, here is an applied example, versions of which show up in all kinds of places (economics, physics, probability, computer science…).

Let’s suppose that we have some sort of system where agents can be in two states, let’s call them states 1 and 2. At time 0, we have a bunch of agents in state 1 and a bunch of agents in state 2. Then, in each time step, some proportion of the agents will flip states.

This setup could be used for demographics and economics: for example, state 1 could be urban residents and state 2 rural residents; each year some proportion move from on state to the other. For another example, in physics, an ammonia molecule can be in one of two main energy states, and its flipping back and forth is responsible for being able to create an “ammonia maser”.

Of course, there’s no limitation on the number of states, but I’m starting with just two states so that things are simple to write down.

Let’s use $x_j(t)$ to denote the number of agents in state $j$ at time $t$. So we start with $x_1(0)$ agents in state 1 and $x_2(0)$ agents in state 2.

Now, let me pick some numbers (arbitrarily). Let’s say that, in each time step, a proportion $0.10$ (that is, 10%) of the agents in state 1 move to state 2, and in each time step, a proportion $0.05$ (that is, 5%) of the agents in state 2 move to state 1.

We can illustrate the situation as follows:

This picture is called a “directed graph” (not to be confused with “graph” like “graph of a function”). That states are called “vertices” or “nodes”, and the lines between the states are called “edges”. If we had more states, we would have a bigger directed graph.

Sometimes people will also indicate the proportions which stay in the state they were in during each time step. Since 10% of the agents in state 1 leave in each time step, 90% of them stay, and similarly for state 2. We could draw it like this:

Note that the number of agents are conserved: agents are not born or killed. We could consider models where that happens, too! But the class of models where the number of agents is conserved are the ones I’ll consider first. These are called “Markov chains”.

It is maybe worth mentioning that, instead of having a bunch of agents, I could also just have one agent, who, each time step, randomly either switches states or stays in its state. Then I would make $x_1(t)$ and $x_2(t)$ be the probabilities that the agent is in state 1 or 2, respectively, at time $t$. You could also imagine this as an agent randomly walking around on a graph, according to assigned probabilities.

A Markov chain: setting up the equations

Alright, now that I’ve told you the assumptions, let’s set up the equations.

Understanding Exercise: Setting up Markov chain equations
Before you read on, try this yourself. Let’s say the time steps are $t=0,1,2,\dotsc$. Write the equations for $x_1(t+1)$ and $x_2(t+1)$ in terms of $x_1(t)$ and $x_2(t)$, with the assumptions about probabilities that I made above. Once you have the equations, try to rewrite them in matrix form.

Got it?

Here’s the answer in linear equations form:

$x_1(t+1)= (0.90) x_1(t) + (0.05) x_2(t)$
$x_2(t+1)= (0.10) x_1(t) + (0.95) x_2(t)$

In matrix form, we could write this as

$\begin{bmatrix}x_1\\x_2\end{bmatrix}(t+1)=\begin{bmatrix}0.90&0.05\\0.10&0.95\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}(t)$

The matrix here,

$T=\begin{bmatrix}0.90&0.05\\0.10&0.95\end{bmatrix}$

is called the transition matrix.

It is often useful, in the equation, to separate out the number of agents from the previous time step, plus the change during the time step. That is, I would rewrite the equation above as

$\begin{bmatrix}x_1\\x_2\end{bmatrix}(t+1)=\begin{bmatrix}x_1\\x_2\end{bmatrix}(t)+\begin{bmatrix}-0.10&0.05\\0.10&-0.05\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}(t)$,

which I could simplify as

$\begin{bmatrix}x_1\\x_2\end{bmatrix}(t+1)=\left(I+\begin{bmatrix}-0.10&0.05\\0.10&-0.05\end{bmatrix}\right)\begin{bmatrix}x_1\\x_2\end{bmatrix}(t)$,

where $I=\begin{bmatrix}1&0\\0&1\end{bmatrix}$ is the $2\times 2$ identity matrix.

Understanding Exercise:
Check that my rewriting of the equation is the same as the original (if I did it correctly!), and make sure you understand the meaning of the terms.

In this case, we would call the matrix which gives the changes in each time step,

$\Delta=\begin{bmatrix}-0.10&0.05\\0.10&-0.05\end{bmatrix}$,

the “difference matrix” or weighted graph Laplacian. Then,

$T=I+\Delta$.

A Markov chain: questions

Given these equations, we could start with any initial number of agents $x_1(0)$ and $x_2(0)$ in the two states 1 and 2, and see how they evolve over time. This would be a little tedious to do by hand, but easy enough with a computer.

One initial thing we might want to know is: does the system approach a steady state, i.e. an equilibrium? That is, do the numbers $x_1(t)$ and $x_2(t)$ settle down over time? Or do they oscillate forever?

Computing Problem: Two-State Markov Chain Example
For those of you who are interested in computing things, this would be a good example to start with. You probably have a preferred system for doing matrix computations already; if you don’t, you might try https://www.sagemath.org/, which combines Python with a Maple-like front end. Try some arbitrary starting values $x_1(0)$ and $x_2(0)$, and then find $x_1(t)$ and $x_2(t)$ for $t=1,2,3,\dotsc$. In particular, find these for fairly large values of $t$: do they in fact settle down, or do they oscillate? Try experimenting with the initial values: how does the behavior depend on what initial values you take?

If you do decide to do this computing exercise, you might want to try it before trying for theoretical answers in the next exercise:

Problem: Finding Two-State Markov Chain Steady State
a) Try to set up equations to determine if this two-state Markov system has a steady state. Assume the same probabilities as above. You might also want to assume some specific numerical values for $x_1(0)$ and $x_2(0)$, at least at first.
b) Try to solve for the steady state. Does the system have a steady state? If it does, check your answer!
c) How does your answer depend on the initial values $x_1(0)$ and $x_2(0)$? If you picked specific numerical values at first, try doing it with unspecified variables instead. Does the nature of the solution depend on the initial values?
c) Can you explain how this question is related to eigenvectors and eigenvalues?

Theory Problem: General Two-State Markov Chains
For those of you who are more theoretically inclined:
a) Do the previous problem, still with two states, but with general transition probabilities replacing the specific ones that I gave in my example. Give a general answer in terms of variables.
b) Can you prove when the system will have a steady state? Can you give a proof which would generalize to more than two states?

We might be interested, not only in the existence and nature of a steady state, but also how the system approaches a steady state. If you’ve done the other problems, here’s a challenge problem to think about: the state of the system at time $t=n$ is going to be given by

$\begin{bmatrix}x_1\\x_2\end{bmatrix}(n)=T^n\begin{bmatrix}x_1\\x_2\end{bmatrix}(0)$.

Can you use what we’ve done above, to find a simpler way of computing $T^n$, so that you can simply find out the state of the system for large time, without having to do a huge number of matrix multiplications?

More answers and explanations next time!

Hi!

Welcome to the new system!

I’m still figuring out how best to make the online thing work. (Once I figure it out, we’ll be back to in-person anyway!) I think the feedback meetings are valuable, but they were difficult to sustain in this format. So my new plan is to suspend the feedback meetings for now, and to spend time making lectures in this written format.

My hope is that the written format will give you something easier to refer to as you are working through the material. Also, I hope it will make it easier to work on your own. One of the hardest things with the online learning for me has been that it is difficult to have all of you work effectively during class time.

Having the core lecture in written format will free us up to use class time more flexibly, hopefully.

Finally, there is a lot more material I’d like to cover than we will have time for in the term. Writing the lectures will give me more of a chance to make optional side trips, which you can choose to follow based on what interests you.

The story so far

OK, let’s get started! Let me start with a brief recap of where we are so far, and then I’ll explain my plan going forward.

Projections

We opened the class with the problem of projections. This has been the theme for the first half of the class.

To begin with, I imagined that you have a given vector $\vec{v}$ in $\mathbb{R}^3$, and a plane $S$ spanned by two given vectors $\vec{u}_1$ and $\vec{u}_2$, and I asked how to find the perpendicular projection $P\vec{v}$ of $\vec{v}$ onto the plane $S$.

I think this problem has worked out pretty well! Even if you did not get a full solution, I think it helped everyone orient themselves and think about what they knew and what they were trying to do. Also, people came up with several different strategies, all of which we are going to use in various situations!

My intention was that you make an initial to solve this problem with things you knew already. Then I would start the strictly logical development of the theory, and I would use the problem as a motivation for and guide to introducing new theory, which we would use to solve the problem different ways.

So far, this problem has been given two solutions. One way was sketched out in Problem Set 3, Problem #1. It depended on the dot product (or more generally, inner product), which we haven’t formally introduced yet. The second way I discussed in class on Tuesday March 30. The second way required us to find a perpendicular subspace, which I also haven’t formally introduced yet.

In the logical development, I am trying to avoid using the inner product as long as possible. The purpose of this is to make clear what doesn’t depend on the inner product, and what actually needs it. In some applications, we don’t have a natural inner product, or we have more than one.

Least Squares

I introduced one major application of projections: “least squares”, which is a way of fitting a line (or curve, or subspace) to some data points in the “best” possible way. This was developed in Problem Sets 1 and 2.

I thought it was important to see a real application early on! Otherwise this all gets too abstract.

Logical Development: Fields, Vector Spaces, Bases, Linear Transformations

While still thinking about the projection problem, we have then started on the development of the subject in strictly logical order. Logically, it would have made sense to start here, but I was worried that it would be too abstract, and it wouldn’t be clear where it was going. My intention was to give a major practical and theoretical problem (projection), and get you to try it on your own first, so that the general theory would be motivated. But of course the general theory is important for a lot else as well.

Most of Problem Sets 3 and 4 are about the logical development of the fundamental concepts.

A Big Problem For The Second Half: Spectral Decomposition and Decoupling

Just last class (Friday April 2), to start off the second half of the term, I introduced another large motivating problem. Actually, I didn’t quite get there yet: we will get to the main idea and problem in class today (Tuesday April 6).

The plan going forward!

I am introducing the “spectral decomposition and decoupling” problem as a motivation, and I will ask you to spend a bit of time thinking about it, but I am not going to get you to struggle through it on your own, the way I did with the projection problem.

From now on, I want to concentrate mostly on the development in logical order. I will still be splitting between theory and applications, but I’ll bring up the applications when we get to them in logical order. There will be more opportunities now for computational problems, for those of you who are interested in that.

In the written lectures, I will start with reviewing the material we have done so far on fields, vector spaces, bases, and linear transformations, adding some more optional theory and applications along the way. Then I will discuss the projection problems and spectral decomposition problems, and then we’ll move forward to new theory and applications.

Here is the list of topics I hoped to cover in this class. We definitely won’t get to everything, but I’m going to try to briefly touch on all of it, at least in optional lectures and problems. I’ve listed them in logical order, but I may jump out of that order a bit, in order to be sure to get to the most important things.

• Fields (including complex numbers, finite fields, rational field extensions)
• Vector spaces (including function spaces, spaces of polynomials, field extensions, functions on graphs/networks, logical operations, families of subsets)
• Subspaces (things we are projecting to, with examples in all the vector spaces listed above)
• Quotient spaces (optional, but important for theory and for computer graphics)
• Projective spaces
• Linear independence, span, and bases (including Legendre and Hermite polynomials, Lagrange interpolation for curve-fitting)
• Direct sums, complementary subspaces, and projections
• Linear transformations
• Dual spaces
• Basis change
• Gauss-Jordan elimination and systems of linear equations
• Decomposition of projections into tensor products
• Decomposition of linear transformations into tensor products
• Image, kernel, and cokernel
• Parametric and scalar equations
• Error-correcting codes
• Eigenvectors, eigenvalues, and spectral decomposition
• Principal component analysis
• PageRank
• Multilinear functions and tensors; Einstein summation notation
• Inner products
• Quadratic forms
• Orthogonal projection
• QR decomposition
• Singular value decomposition
• Jordan decomposition
• Determinants
• Tensors
• Differential forms

What next?

I will keep posting written lectures. I am planning to start with a recap of the material on fields, vector spaces, bases and linear transformations. I will let you know on the Slack when a new one is posted, and I will list them all on the Advanced Linear Algebra main page.

The written lectures will include problems, which I recommend doing as you work through the lecture, but which I am not asking you to hand in.

I will let you know, on Slack, what are the main things I’d like you to be working on, and what the suggested due dates are for submitting problems.