What about other polyhedra, beyond the cube? What is geometry like there?
The Regular Tetrahedron
The surface of this polyhedron consists of 4 equilateral triangles. There are 3 triangles meeting at each vertex, and a total of 4 vertices.
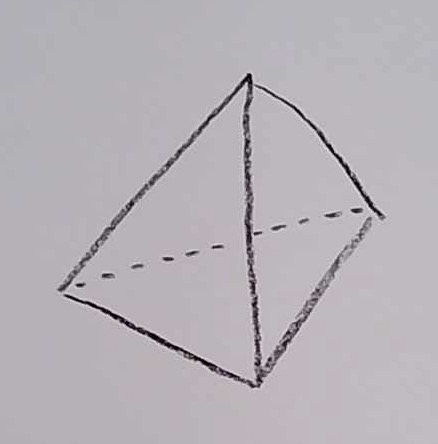
You can make a model of a vertex by taking three equilateral triangle, and gluing them together as follows:
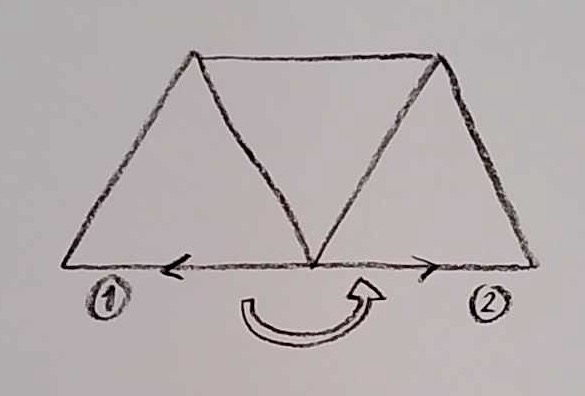
I would recommend that you do this with paper, scissors, and tape. (Light cardboard can make an even better model.)
(For the moment, I am only concerned with the regular tetrahedron, so I will sometimes just say “tetrahedron” for short, and you should take that to mean “regular tetrahedron”. It would be “irregular” if it had four triangular faces arranged as above, but if the faces weren’t all equilateral, and/or if the vertices did not look the same. I won’t worry about “irregular” tetrahedra right now. The same point goes for the other polyhedra described below: assume regular, unless specified otherwise.)
Problem 1: Suppose we pick a point A in the triangular face on the left of the diagram above, and we start drawing a line which hits Edge 1 at point P. This line will reappear at a point Q on Edge 2. Give rules for where the line will appear, and at what angle it will be going (similar to what we did for the cube).
Problem 2: Draw a triangle on the regular tetrahedron that contains one vertex (by drawing it on the flattened model as shown above). Try to pick the simplest triangle you can. What does it look like on the three-dimensional tetrahedron? What is its internal angle sum?
Problem 3: Find the internal angle sum for any triangle which contains one vertex. (Give an argument like one of the ones I gave for triangles on the cube.)
Problem 4: Suppose we draw a circle in Tetrahedronworld, whose radius is r, and whose center is on a vertex. What does it look like? What is the formula for its circumference? (Assume that r is less than the distance to the next vertex, otherwise things get quite complicated.)
The Octahedron
The surface of this polyhedron consists of 8 equilateral triangles, with 4 triangular faces meeting at each vertex. There is a total of 6 vertices.
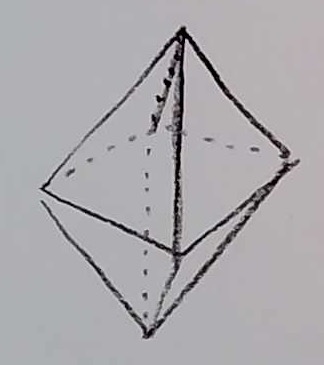
You could also think of this as two square-based pyramids, glued together at their bases, and then erasing the bases in the middle. You can make a model of one vertex of the regular octahedron by drawing four equilateral triangles, and gluing together as follows:
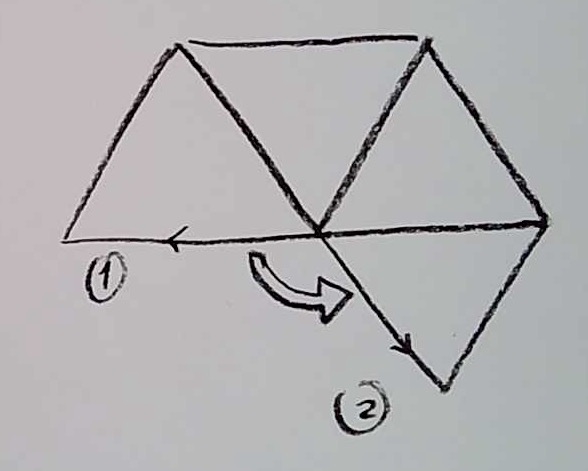
I would recommend you make a model for yourself, with paper, scissors, and tape.
Problem 5: This is actually multiple problems. I would like you to do all the same problems you did for the regular tetrahedron, again for the regular octahedron. That is:
– Give the rule for a line leaving Edge 1 and appearing from Edge 2
– Draw a simple triangle containing one vertex, and find its angle sum
– Prove that any triangle containing one vertex has that same angle sum
– Draw a circle, and give the formula for its circumference
You can be a bit less detailed this time; you can concentrate just on the features that are different between the regular tetrahedron and the regular octahedron.
The Regular Icosahedron
The regular icosahedron has a surface consisting of 20 equilateral triangles, with 5 triangles meeting at each vertex. There is a total of 12 vertices.
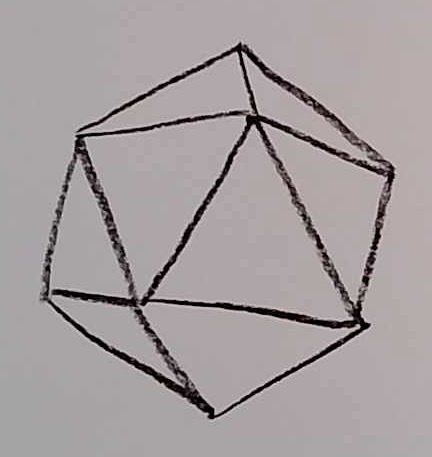
Problem 6: Make a model of a vertex of a regular icosahedron. Answer all the questions for the regular icosahedron that you did for the tetrahedron and octahedron above. (So this question is also multiple problems.)
The Regular Dodecahedron
This polyhedron has 12 faces, each of which is a regular pentagon (5-sided polygon). There are 3 pentagons meeting at each vertex. There is a total of 20 vertices.
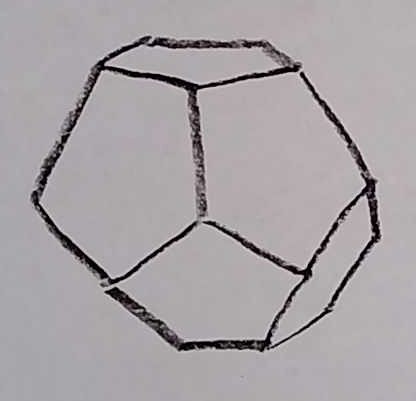
Problem 7: Exactly like Problem 6, except for the dodecahedron.
The Platonic Solids
Let’s call a polyhedron regular if:
- every face is a regular polygon;
- every face is congruent; and
- a neighborhood of every vertex is congruent.
That last condition means that, for example, if one vertex has four triangles meeting there, then every vertex should have four triangles meeting there, and moreover, if I took a little region around the first vertex, I could exactly overlay it over the same region on the second vertex. (This definition isn’t totally sharp, but we can make it better later.)
It is a remarkable fact that there are only five regular polyhedra possible! These are called the Platonic Solids.
Problem 8: Try to think of a reason why the regular polyhedra we have listed above are the only ones possible. (It may help to classify them by type. For example, you can try to explain first why no other triangle-faced regular polyhedra are possible.)
There are many more polyhedra out there, though. If we pick a less restrictive class than “regular”, then we can give more examples. For example, we could still ask that every vertex looks the same, and that every face be a regular polygon, but we could drop the condition that all faces are congruent. So, for example, you could have a polyhedron whose faces are a mix of equilateral triangles and squares. A polyhedron satisfying these conditions is called an Archimedean solid.
Problem 9: Try to come up with an example of an Archimedean solid (which is not a Platonic solid). (If you are feeling ambitious, you can try to come up with as many examples as possible. You could even hazard a guess at how many Archimedean solids there are in total.)
