In this lecture, I want to talk about the Möbius strip and its cousins, the non-orientable 2D spaces. (And I want to talk about what “orientable” means.)
I’ve talked with you in class about some of these things; I want to back that up here, and to provide some more details. Then I want to go a bit further. The relevant text for this is The Shape of Space, Chapter 4.
The Möbius Strip
Let’s recall the Möbius strip. There are two different spaces I have been talking about, and I’ve been calling them both the “Möbius strip”, so let me set the record straight here.
Actually, while I’m at it, I’ve been calling two different spaces the “cylinder”, so let me come clean there as well.
On the one hand, I can start with an infinite strip in the 2D Euclidean plane, bounded by two parallel lines on its sides, and I can “glue” the left side to the right side:

This can be embedded in 3D, as the surface of an infinitely long, straight, circular tube:

I will call that one the “infinite cylinder”.
On the other hand, I could start with a rectangle, and glue together two of the sides, keeping the orientation straight:

This one I’ll call the “finite cylinder”. It also has a uniform locally Euclidean geometry, but it is finite in extent, and it has a boundary, consisting of the top and bottom edges. A 2D inhabitant of this universe can “fall off the world”.
I can embed this in 3D in the most straightforward way, as the side surface of a 3D, straight, circular cylinder:
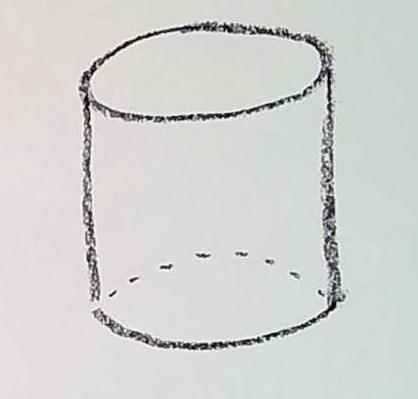
In this picture, I am assuming that the surface is a hollow tube; I am NOT capping it off with a top and bottom. (If I did do that, I would get a different space; let’s call it the “closed finite cylinder”. How does that space sit in the classification of the last lecture? What is geometry like in that universe?)
There are other ways to embed the flat 2D cylinder into 3 dimensions:

It took me a few tries to get that second picture right! (At least, I think it’s right now. You should check my work!)
OK, so back to Möbius strips! There will be two versions, the infinite Möbius strip, and the finite Möbius strip. I am going to glue the sides with a reversal of orientation. For the infinite Möbius strip, I will have to pick a center line of this reflection, say PP’, where P and P’ are points on the left and right edge respectively, at the same height. Any point Q on the left side above P will be identified with a point Q’ at the same distance below P’ on the right side:
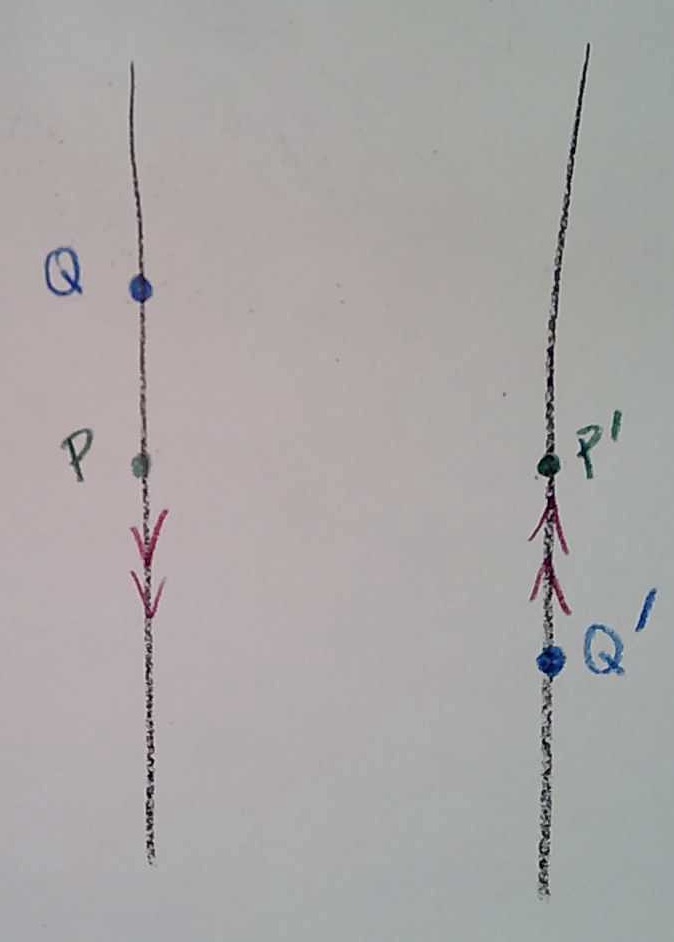
I can’t embed this infinite Möbius strip in 3 dimensions, without having it self-intersect. (That can be proved, but it isn’t easy!)
For the finite Möbius strip, since the left and right edges are finite line segments, reversing the orientation makes the center line the middle of those line segments:
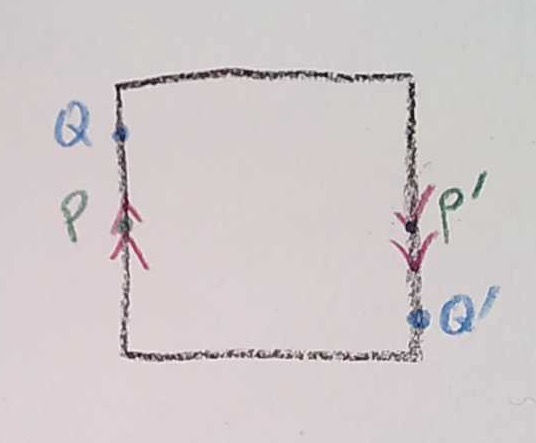
The finite Möbius strip, in contrast, can be embedded in 3 dimensions, in a number of ways:

Problem 1:
a) Where do these two types of Möbius strips fit in the classification of Lecture 4?
b) Describe the boundary of the finite Möbius strip. (Careful, this is a trick question!)
c) In the picture I drew earlier, where I embedded the 2D cylinder in three dimensions as a knotted strip: how could I change this to make it into an embedding of the 2D Möbius strip?
Problem 2:
In class, I made a Möbius strip out of paper (that is, a 2D finite Möbius strip, embedded in three dimensions in the most straightforward way). Then I cut it down the center. For another experiment, I cut it on two lines, 1/3 and 2/3 the way up the strip.
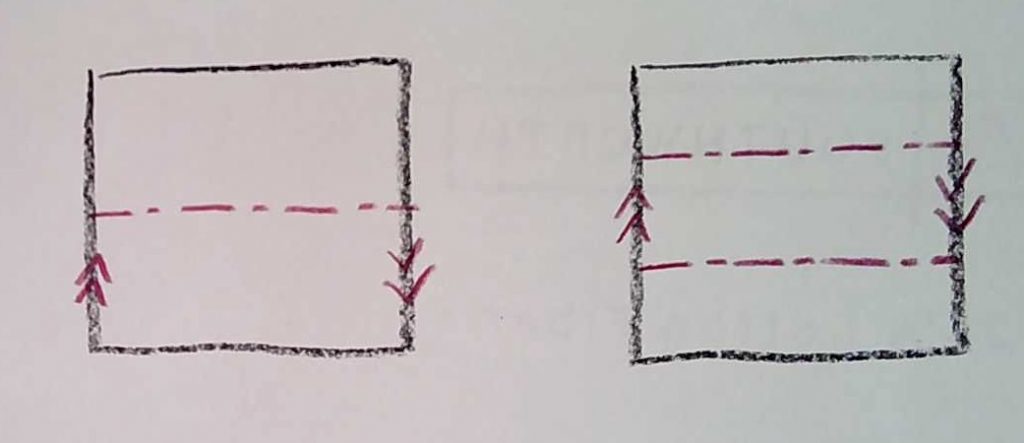
Experiment! Do it physically, with paper and tape and scissors. Try more possibilities with the cutting line. What can happen? Can you find a pattern? If you can find one, can you explain it? The result has multiple features (number of pieces, how each is twisted, how they are linked). Can you explain the pattern in each of these features? Can you generalize further to other possibilities? (For example, what if I start with a cylinder with a double (360 degree) twist in three dimensions, and do the same thing?)
(Hint: At least for understanding the pieces intrinsically, you could try starting with the 2D picture of the strip with the gluing rules, and cut and paste that 2D picture (re-labeling the gluing rules as needed).)
The Klein Bottle
If we start with the finite Möbius strip, we can then choose to glue together the top and bottom:
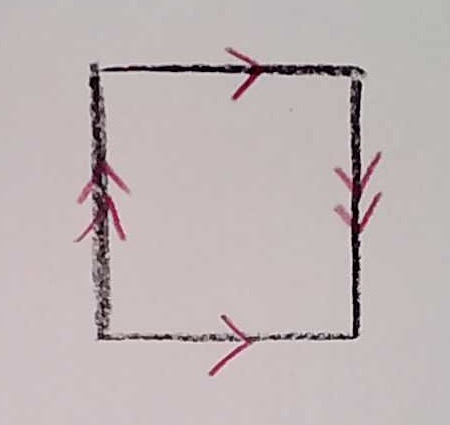
We cannot embed the Klein bottle in three dimensions. Not without intersections, anyway. If we try, we can see how close we can get, and why it seems not to be able to work. Start by gluing together the two edges with matching orientations, to make a cylinder. Then, try to stretch around the edges to glue together the end circles, as we did for the torus:
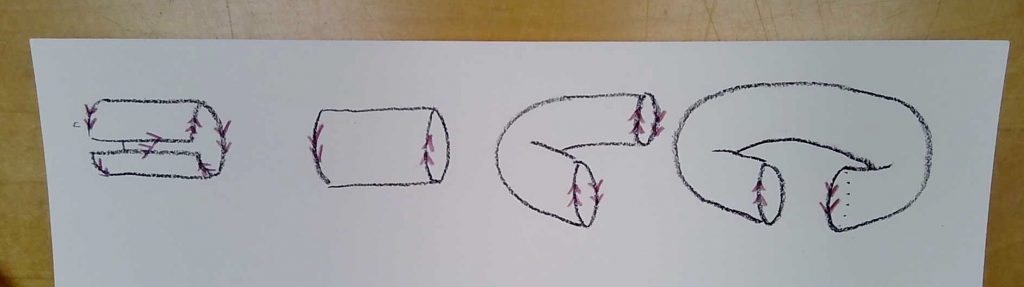
The arrows are pointing the wrong way! For the torus, I could have just glued them together straight. Now, I have to turn one of the arms around to make the orientations match.
And that’s where we encounter our problem: to then glue them, I need to get at the other circle from inside the tube. The only way is to cut a slice into the one arm, so I can pass the other arm through:

I have a tough time drawing the final result, so I’ll refer you to the book for that picture. We can sort of think of this as an embedding, if we make the rule that 2D creatures do not see the slice cut in the arm; they just pass across it without noticing. (The two edges of the slice are abstractly “glued”.)
Incidentally, I’ve been talking throughout of a mental image of surfaces being “paper”, and joining edges being “gluing”. But when we are stretching and cutting as we are, it might be better to imagine the surfaces as some sort of fabric: maybe knitted sweater material, or T-shirt fabric, and to imagine joining as sewing. (Of course, these are all mental images to help us think about the idealized mathematical surfaces, which have no thickness at all.)
Problem 3:
Where does the Klein bottle fit in our classification from the last lecture?
Problem 4:
(This might be a longer “research” type question.)
I’d like to try cutting the Klein bottle down the middle with scissors, like we did for Möbius strips! There is a slight difficulty: to do it with paper and scissors, we’d have to work in four dimensions. But we can still perform the cutting with the abstract, intrinsic diagram of the Klein bottle. The interlinking or embedding of the pieces doesn’t make much sense anymore, but we can still figure out what each piece is intrinsically.
a) Cut the Klein bottle down the middle with scissors:
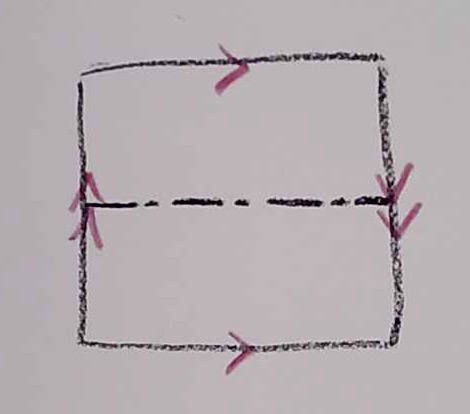
The result will be two surfaces (or maybe one surface) with a boundary (the edge created by the cut). What are(is) those(that) surface(s)?
b) Now try cutting on a line 1/3 of the way up and 2/3 of the way up.
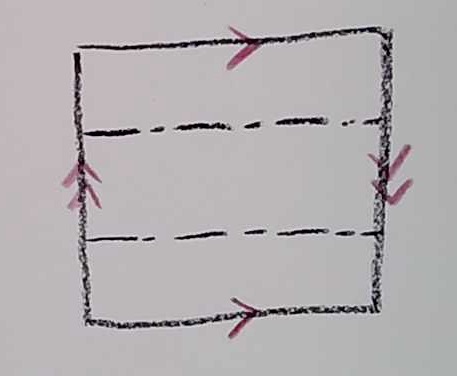
How many surfaces? What are they?
c) Continue with this process. Can you determine a rule or pattern?
d) I guess I should have started doing this with the torus, which presumably would have been easier. Try cutting the torus (abstractly) in the same way. What surfaces result in each case? What is the pattern?
Problem 5:
(This might also be a longer “research” type question. I’d like everyone to at least try to get started on it, but you can consider going into more depth as being optional.)
In an earlier problem, you analyzed the possibilities for a straight line (geodesic) on the flat 2D torus (assuming a square shape). We got a fairly detailed answer: if the slope is a rational number, then the numerator and denominator determine how many times the straight line wraps around in the two directions before closing in on itself (closed geodesic). If the slope is an irrational number, the straight line never meets itself, and continues forever.
I’d like you to try to do a similar analysis of the straight lines (geodesics) on the flat 2D Klein bottle. Start by drawing some simple closed straight lines, to see if it is even possible. Build up some examples by experiment. Then, try to work toward a more systematic answer.
Other Possibilities??
Starting with a flat 2D square, we have glued the sides in different ways to produce a cylinder, a Möbius strip, a torus, and a Klein bottle. Are there other ways to glue the sides of a square that we haven’t tried? If there are, do these even make sense as surfaces? If so, what do they look like?
Problem 6:
Try to answer the questions above. First, try to enumerate all the fundamentally different ways we could identify edges of a 2D square. (You’ll have to decide what “fundamentally different” ought to mean.) Then, for each possibility, go through the analysis we have done above for the cylinder, Möbius strip, torus, and Klein bottle: figure out if you can embed it in three dimensions (maybe with some cheating). Figure out what the geometry and topology is: is it flat? Does it have a boundary? Classify it according to the previous lecture. Maybe some options just reproduce what we’ve done before; if so, explain why. Maybe some options just don’t make sense as surfaces; if so, explain why.
The End of This Lecture…
Well, that was fun!

Next time, I’d like to do more cutting and pasting: punching holes in surfaces, sewing them together. I’m also heading towards doing 3D spaces, analogously to how we’ve been doing 2D spaces. And I want to get back to geometry and curvature, and how that is related to the topology of a space. I’d encourage you to keep thinking of questions and imagining other possibilities as we move forward!
