Geometry Lecture A (supplementary): Proportions, not formulas!

This is a little bit out of the sequence of lectures, so I am numbering it as a “supplementary” lecture. I’ll probably continue doing this when I need to make side points.

On Problem Set 5, I noticed that many people had remembered, or looked up, formulas to convert from radians to degrees, or formulas for arc length. Although this gives correct answers, I think it is very important to understand that this is unnecessary! All those things can be worked out by proportions.

One of the main things I want to get across in this class, is that you don’t have to memorize formulas, or take things on authority. You can figure them out yourself. And moreover, figuring them out yourself is often easier, and gives you a better understanding.

If you were already doing these problems by proportions, you can skip this section; though it might be good to skim through it and see if there is anything new to you. However, if you had used formulas for converting degrees to radians or finding arc lengths, I would like you to work through this section and do the problems. This is an important thing to work out.

I also make some comments about how to algebraically deal with fractions in this lecture; you should take a look and see if this is helpful.

What you DO need to memorize

OK, let’s get started. There is one formula you need to know: that the circumference of a circle C (the distance around its edge) is related to its radius r (the distance from the center to any point on the edge) by

$C=2\pi r$ .

(ASIDE: Where does this formula come from? Well, it contains two things. One, it is implicitly asserting that the ratio of the circumference of a circle to its radius, the ratio C/r, is the same for any circle. That part is actual math. The other part of this formula is a convention; assuming that this ratio is in fact constant, we are naming that constant, $\dfrac{C}{r}=2\pi$ . In other words, that defines what we mean by $\pi$ . Why the 2? Well, historically, people tended to work with the diameter rather than the radius, so they wrote this formula $\dfrac{C}{d}=\pi$ , or equivalently $C=\pi d$ .)

There are also two conventions you need to know: the angle all the way around, coming full circle, is by convention 360 degrees (for historical reasons), or $2\pi$ radians (for math reasons we will see as we go on).

Converting between degrees and radians

You do not need a conversion formula between degrees and radians. You can figure it out by proportions. Let’s say we have some angle $a$ . I can measure that angle in degrees, or in radians. I’m going to distinguish these two different numbers by writing them $a_{\mathrm{deg}}$ and $a_{\mathrm{rad}}$ respectively.

The proportion $a$ is of a full rotation shouldn’t matter how we measure it! That is:

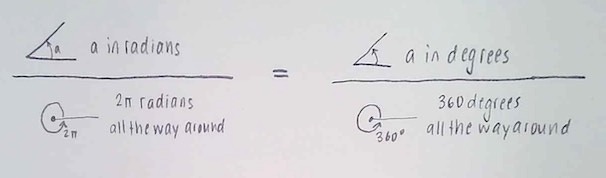
What proportion angle a is of a full rotation should be the same either way!

Written in a more condensed way, this says

$\dfrac{a_{\mathrm{rad}}}{2\pi}= \dfrac{a_{\mathrm{deg}}}{360^\circ}$ .

Now, let’s say you know $a$ in degrees, and you want to find $a$ in radians. So you need to solve for $a_{\mathrm{rad}}$ . I’m going to walk you through this in a long-winded way, in case you don’t remember algebra well. Even if you do, I think the method I suggest to think about fractions can be useful.

What I suggest for fractions is this: instead of being a division, think of every fraction as being a multiplication by a reciprocal. This is what we do in advanced math, and it’s helpful even for simple algebra problems. (The underlying reason is that division is a terrible operation, just awful. For example, it is NOT true that $(a\div b)\div c$ is equal to $a\div(b\div c)$ (try it!).)

So, I’ll write the formula above as

$\dfrac{1}{2\pi}\dfrac{a_{\mathrm{rad}}}{1} = \dfrac{1}{360^\circ}\dfrac{a_{\mathrm{deg}}}{1}$ ,

because, remember, that you multiply fractions by multiplying the tops and bottoms. Dividing a number by 1 doesn’t change it, so we can write this more simply as

$\dfrac{1}{2\pi}a_{\mathrm{rad}}= \dfrac{1}{360^\circ}a_{\mathrm{deg}}$ .

When I see a formula like $\dfrac{a_{\mathrm{rad}}}{2\pi} = \dfrac{a_{\mathrm{deg}}}{360^\circ}$ , I automatically read it as $\dfrac{1}{2\pi}a_{\mathrm{rad}} = \dfrac{1}{360^\circ}a_{\mathrm{deg}}$ (which is standard in advanced math).

OK, now that makes it clear how to solve for $a_{\mathrm{rad}}$ : I have to multiply both sides by $2\pi$ :

$2\pi\times\dfrac{1}{2\pi}a_{\mathrm{rad}}= 2\pi\times\dfrac{1}{360^\circ}a_{\mathrm{deg}}$ ,

$a_{\mathrm{rad}}= \dfrac{2\pi}{360^\circ}a_{\mathrm{deg}}$ .

(Remember what I said about fractions; I could convert $2\pi\times\dfrac{1}{360^\circ}=\dfrac{2\pi}{1}\times\dfrac{1}{360^\circ}=\dfrac{2\pi}{360^\circ}$ . More simply, I just read $\dfrac{2\pi}{360^\circ}$ automatically as meaning $2\pi\times\dfrac{1}{360^\circ}$ , basically by definition.

(If you have done “cross-multiplying” in the past, please forget about it. It’s technically correct, but it is confusing, and it is NEVER necessary. All algebra consists of doing the same thing to both sides of an equation.)

Now, we can simplify the fraction $\dfrac{2\pi}{360^\circ}$ as follows:

$\dfrac{2\pi}{360^\circ}=\dfrac{2\times\pi}{2\times 180^\circ}=\dfrac{2}{2}\times\dfrac{\pi}{180^\circ}=1\times\dfrac{\pi}{180^\circ}=\dfrac{\pi}{180^\circ}$ .

So, the formula above can be written more simply as

$a_{\mathrm{rad}}= \dfrac{\pi}{180^\circ}a_{\mathrm{deg}}$ .

This is the formula you may have found for converting degrees to radians. I wouldn’t suggest memorizing this formula—I haven’t. Instead, it is easier and more instructive to go back to the proportions every time.

Note that I have done the algebra in a ton of detail above. I have done this so that, if you are rusty on algebra, you can follow through the steps carefully. If you are rusty on algebra, I would recommend that you do many explicit steps, like I have above, until it starts to feel boring. But once you are comfortable, you can skip all these steps, and jump straight from $\dfrac{a_{\mathrm{rad}}}{2\pi} = \dfrac{a_{\mathrm{deg}}}{360^\circ}$ to $a_{\mathrm{rad}}= \dfrac{\pi}{180^\circ}a_{\mathrm{deg}}$ .

Problem 1: Suppose that you know an angle in radians, and you want to convert it to degrees. Follow similar steps as above, to solve for $a_{\mathrm{deg}$ in terms of $a_{\mathrm{rad}$ .

Problem 2: Convert $\dfrac{\pi}{6}$ radians to degrees. Don’t use the formula you worked out; instead, go back to the proportions and work it out from there. (Hint: You’ll get a fraction over a fraction at first. But rewriting the big fraction in the way I recommended will eliminate this potential problem.)

Problem 3: Convert 120 degrees to radians. Don’t use the formula I worked out above; instead, go back to proportions and work it out from there.

Finding arc lengths on a circle

Now, let’s suppose that I know an angle $a$ , which I have placed at the center of a circle, of known radius r. I want to figure out the length s of the arc of the circle that is cut out by this angle. I gave a formula in class, and some of you looked up a formula, but this is not necessary. You can, and should, work it out by proportions.

Let me assume that the angle is given in radians. (I’ll ask you how to work this out if the angle is in degrees, in the problems.)

The proportion that the angle $a$ makes of a full rotation, should be the same as the proportion that the arc length s makes of the length all the way around, i.e. of the circumference:

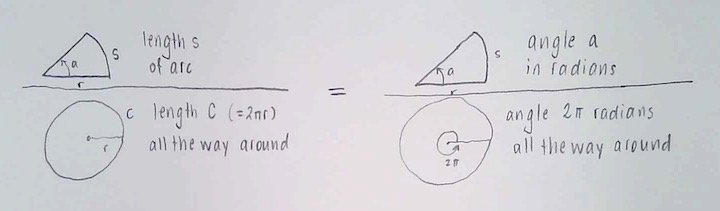
Written more compactly, this says

$\dfrac{s}{2\pi r} = \dfrac{a_{\mathrm{rad}}}{2\pi}$ ,

which simplifies to

$\dfrac{s}{r} = a_{\mathrm{rad}$ .

Problem 4: Fill in the details of simplifying $\dfrac{s}{2\pi r} = \dfrac{a_{\mathrm{rad}}}{2\pi}$ to $\dfrac{s}{r} = a_{\mathrm{rad}}$ .

Problem 5: Suppose we know that an angle $a$ cuts out a length of 6 on a circle of radius 2. Find the angle $a$ in radians.

Problem 6: What I did above means that, if you know the radius r of the circle, and the arc length sof a piece of a circle, you can calculate the corresponding angle $a$ in radians. Suppose instead that I know the angle and radius, and I want to find the arc length. How do you have to rearrange the formula? Do so.

Problem 7:
a. Suppose that we have a circle of radius 5, and suppose we draw an angle at the center of size 1 radian. How long of an arc does that angle cut out on the circle?
b. Same question, but change the angle to size $\dfrac{\pi}{4}$ radians.

Problem 8:
a. Repeat what I did above, but assume now that the angle $a$ is given in degrees rather than radians. Find a formula that relates the angle $a_{\mathrm{deg}$ , given in degrees, to the arc length s and radius of the circle r. Simplify as much as you can.
b. Compare the formula that you just got for $a$ in degrees to the equivalent one we got for $a$ in radians. Which looks nicer? This should hopefully give you an initial sense of why radians will work out more simply than degrees. (There will be more important simplifications from working in radians as we move on. Of course, we can always convert any formula involving radians into an uglier one involving degrees if we need to.)

What you DO need to memorize

Converting between degrees and radians

Finding arc lengths on a circle

Leave a Reply Cancel reply